03-01-2021, 03:51 PM
The successive approximation converter is a good choice for for fast data rates. The concept is simple - incrementally improve a digital approximation of an analog input by testing one bit at a time. You start with the most significant bit, and compare to see if the input to be digitized is above or below half scale. After the first bit is left set or cleared, you then set the next bit, and compare again, leaving the next bit set or clear. The process continues for the number of bits in play. Normally, a person would use an A/D chip which does most of the job. That is fine, as far as it goes, but if you want to actually understand the process, instead of just using a chip, you need to reinvent it for yourself. That is likely too much time, cost, and effort on the bench, but in SPICE you can get the full picture with a little thought, and maybe some virtual tinkering.
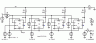
If you were to build this sort of of circuit on the bench, it wouldn't look much like this SPICE. You would use an addressable latch to build the answer and a counter to step through the bits. SPICE could simulate that, too, but LTSPICE is fundamentally a linear tool that does not excel at simulating digital ICs. Instead, here we will duplicate the principle using behaviorials. The schematic may not look the same, but the waveforms will, and understanding the waveforms is the heart of understanding the successive approximation converter.
Instead of a counter, we here use a ramp T, based on time, or you could just as well use a sawtooth wave, to create the time base for a series of A/D conversions. Voltage T ramps from 0 to 5 volts every 10 us. A behavioral, B5, generates a start signal when the ramp resets to 0. The first bit decision is made at 1 volt, the second at 2 volts, the third at 3 volts and the last at 4 volts. The answer is held for 2 us while the ramp rises from 4 to 5 volts. For simplicity, we show a 4-bit converter, but adding bits is just a matter of replication and extension of the principle.
If you know what a D-flop is, you can skip this paragraph. The logic element used here to store each of the four bits of the conversion is a type D latch. It is unconditionally set by a one at the preset terminal, PRE, and unconditionally cleared by a one at the clear terminal, CLR. The contents, a one or a zero, is otherwise preserved unless the clock input, CLK, transitions from a zero to a one. The logic level that is present at the data input, D, is then captured and held in the latch. Latch contents are found at output Q, with the inversion of Q found at Q bar (not used here).
The four latches build the 4-bit answer. When the sawtooth ramp resets to zero, behavioral B5, with a formula of V= V(t) < 0.3, produces a start signal. The 0.3 is arbitrary. Anything more than 0 and less than 1 will work. That start signal presets the most significant bit (MSB) and clears the other three bits. That binary 1000 starts the converter off at half scale, Each latched bit drives a binarily-scaled resistor so that the combination of any 4 bits appears as the corresponding analog voltage at point sar (short for successive approximation register). Binary 0000 equals zero volts and binary 1111 equals 15/16th of full scale, full scale being 1 volt in this case. So, binary 1000 is 8/16th, or 0.5 volts. In an actual circuit, scaling of the sar, and the analog input for comparison, would be a matter of the logic family used and other hardware considerations. To illustrate the principle of a successive approximation converter, the scaling just needs to be internally consistent.
Now is when it gets interesting. The comparator, A5, compares the unknown analog input to that 0.5 volts. Once the ramp reaches 1, the first register is latched by clock signal B1. If the analog input is higher than half scale, the comparator output is a one, and the MSB stays set. If the input is lower, the comparator output is a zero, and the MSB is cleared. Because the latches are edge triggered, the data from the comparator is ignored except at the time the clock input transitions from 0 to 1. For the MSB, that happens at time 1, because the formula for the behavioral clock, B1, is V = V(t) > 1.
Next, behavioral B6 determines that the ramp is between 1 and 2. It sets the next bit, b3, by presetting latch A2. That preset occurs regardless of whether the MSB was left set or cleared. The voltage at sar will then be either 3/4 or 1/4 of full scale. The comparator state for bit three represents whether 1/4 or 3/4 is above or below the analog input. Again, if the sar voltage is too high, the comparator output is low and bit 3 is latched clear by behavioral B2 when the ramp reachs 2 volts. Otherwise b3 is left set. The process continues for the last two bits. There are many waveforms on the next illustration, but bear with me.

The input is a 1kHz sine wave, in blue below. You can see 100 conversions per cycle. The output, in red, is a 4-bit analog replica of the input voltage. I will describe how it is derived below. The upper axis is the digital information. The various signals are offset to keep them from overwritting each other. Lowest, in dark blue is the start signal, which flags the beginning of each conversion. Jump up to the top for the MSB, in green. It is constantly set whenever the input is above half scale, and is set briefly, then cleared whenever the input is below half scale. The pink trace is bit three, light blue is bit 2, and gray is the least significant bit.
Pay particular attention the the green trace below, sar. This signal is the analog approximation that is built one bit at a time. For a better appreciation, see the detail below which expands the region near the mid-scale transition.

Just above mid scale, to the left, you see that the MSB is always set. Between 490 and 510 us, the other three bits are all cleared, for a conversion answer of 1000 binary. The next conversion falls below mid scale, and clears the MSB, but sets the other three bits, for a conversion result of 0111. Once you see the logic of it, the sar waveform makes intuitive sense, before you grasp the logic, it looks pretty wild.
The seemingly simple task of capturing each result as a digital word is non-trivial in LTSPICE. One way would be to have a second set of latches and to clock the data from the first set of latches into the second set at the end of each conversion period. That seems like a lot of circuitry for not much. Another approach would be a behavioral which binarily weighed and summed the bits, but wait, we already have a binary summation of the bits in the form of V(sar). What is needed is a sample-and-hold circuit to preserve the sar voltage after the LSB is decided. It is entirely possible to construct an actual sample and hold circuit in LTSPICE with a switch and a capacitor and switch control circuitry, but stray capacitance, stray charge, and turn on and turn off times make it more of a job than it seems like it should be. Instead, behavioral B10, with a resistor and a capacitor, will do the job virtually.
The formula in B10 is: V= if(V(t)>4.1, v(sar), v(out))
We might prefer to skip the resistor and capacitor and just label the behavioral “out”, but that will give a SPICE circularity error. The resistor and capacitor don't particularly filter, they just allow SPICE to succeed. V(out) gets updated to equal v(sar) at the end of each ramp, and is otherwise set equal to itself. (Think of it as an analog D-flop.) That preserves the final sar voltage from each conversion until the next conversion is complete, providing a step-wise reconstruction of the input voltage.
Maybe another day I will describe the R/2R ladder, which is a more practical way to binarily weigh more than handful of bits.
LTSPICE is a valuable tool set, and is available at no cost, so don't let the price stop you.
Download this LTSPICE model at: https://lawsonlabs.com/SPICE_sar/SAR4.asc
In SPICE you can add bits of resolution without worrying about the noise floor. You can speed up the conversion without much regard for the realities of slew rates and settling times. Maybe best of all, you can experiment without worrying about producing a cloud of bad-smelling smoke that lingers in the air. If you do want to build this sort of converter, that would be a different exercise, but the modeling here should give you a good grasp of the underlying methods.
Tom Lawson
March 1, 2021
If you were to build this sort of of circuit on the bench, it wouldn't look much like this SPICE. You would use an addressable latch to build the answer and a counter to step through the bits. SPICE could simulate that, too, but LTSPICE is fundamentally a linear tool that does not excel at simulating digital ICs. Instead, here we will duplicate the principle using behaviorials. The schematic may not look the same, but the waveforms will, and understanding the waveforms is the heart of understanding the successive approximation converter.
Instead of a counter, we here use a ramp T, based on time, or you could just as well use a sawtooth wave, to create the time base for a series of A/D conversions. Voltage T ramps from 0 to 5 volts every 10 us. A behavioral, B5, generates a start signal when the ramp resets to 0. The first bit decision is made at 1 volt, the second at 2 volts, the third at 3 volts and the last at 4 volts. The answer is held for 2 us while the ramp rises from 4 to 5 volts. For simplicity, we show a 4-bit converter, but adding bits is just a matter of replication and extension of the principle.
If you know what a D-flop is, you can skip this paragraph. The logic element used here to store each of the four bits of the conversion is a type D latch. It is unconditionally set by a one at the preset terminal, PRE, and unconditionally cleared by a one at the clear terminal, CLR. The contents, a one or a zero, is otherwise preserved unless the clock input, CLK, transitions from a zero to a one. The logic level that is present at the data input, D, is then captured and held in the latch. Latch contents are found at output Q, with the inversion of Q found at Q bar (not used here).
The four latches build the 4-bit answer. When the sawtooth ramp resets to zero, behavioral B5, with a formula of V= V(t) < 0.3, produces a start signal. The 0.3 is arbitrary. Anything more than 0 and less than 1 will work. That start signal presets the most significant bit (MSB) and clears the other three bits. That binary 1000 starts the converter off at half scale, Each latched bit drives a binarily-scaled resistor so that the combination of any 4 bits appears as the corresponding analog voltage at point sar (short for successive approximation register). Binary 0000 equals zero volts and binary 1111 equals 15/16th of full scale, full scale being 1 volt in this case. So, binary 1000 is 8/16th, or 0.5 volts. In an actual circuit, scaling of the sar, and the analog input for comparison, would be a matter of the logic family used and other hardware considerations. To illustrate the principle of a successive approximation converter, the scaling just needs to be internally consistent.
Now is when it gets interesting. The comparator, A5, compares the unknown analog input to that 0.5 volts. Once the ramp reaches 1, the first register is latched by clock signal B1. If the analog input is higher than half scale, the comparator output is a one, and the MSB stays set. If the input is lower, the comparator output is a zero, and the MSB is cleared. Because the latches are edge triggered, the data from the comparator is ignored except at the time the clock input transitions from 0 to 1. For the MSB, that happens at time 1, because the formula for the behavioral clock, B1, is V = V(t) > 1.
Next, behavioral B6 determines that the ramp is between 1 and 2. It sets the next bit, b3, by presetting latch A2. That preset occurs regardless of whether the MSB was left set or cleared. The voltage at sar will then be either 3/4 or 1/4 of full scale. The comparator state for bit three represents whether 1/4 or 3/4 is above or below the analog input. Again, if the sar voltage is too high, the comparator output is low and bit 3 is latched clear by behavioral B2 when the ramp reachs 2 volts. Otherwise b3 is left set. The process continues for the last two bits. There are many waveforms on the next illustration, but bear with me.
The input is a 1kHz sine wave, in blue below. You can see 100 conversions per cycle. The output, in red, is a 4-bit analog replica of the input voltage. I will describe how it is derived below. The upper axis is the digital information. The various signals are offset to keep them from overwritting each other. Lowest, in dark blue is the start signal, which flags the beginning of each conversion. Jump up to the top for the MSB, in green. It is constantly set whenever the input is above half scale, and is set briefly, then cleared whenever the input is below half scale. The pink trace is bit three, light blue is bit 2, and gray is the least significant bit.
Pay particular attention the the green trace below, sar. This signal is the analog approximation that is built one bit at a time. For a better appreciation, see the detail below which expands the region near the mid-scale transition.
Just above mid scale, to the left, you see that the MSB is always set. Between 490 and 510 us, the other three bits are all cleared, for a conversion answer of 1000 binary. The next conversion falls below mid scale, and clears the MSB, but sets the other three bits, for a conversion result of 0111. Once you see the logic of it, the sar waveform makes intuitive sense, before you grasp the logic, it looks pretty wild.
The seemingly simple task of capturing each result as a digital word is non-trivial in LTSPICE. One way would be to have a second set of latches and to clock the data from the first set of latches into the second set at the end of each conversion period. That seems like a lot of circuitry for not much. Another approach would be a behavioral which binarily weighed and summed the bits, but wait, we already have a binary summation of the bits in the form of V(sar). What is needed is a sample-and-hold circuit to preserve the sar voltage after the LSB is decided. It is entirely possible to construct an actual sample and hold circuit in LTSPICE with a switch and a capacitor and switch control circuitry, but stray capacitance, stray charge, and turn on and turn off times make it more of a job than it seems like it should be. Instead, behavioral B10, with a resistor and a capacitor, will do the job virtually.
The formula in B10 is: V= if(V(t)>4.1, v(sar), v(out))
We might prefer to skip the resistor and capacitor and just label the behavioral “out”, but that will give a SPICE circularity error. The resistor and capacitor don't particularly filter, they just allow SPICE to succeed. V(out) gets updated to equal v(sar) at the end of each ramp, and is otherwise set equal to itself. (Think of it as an analog D-flop.) That preserves the final sar voltage from each conversion until the next conversion is complete, providing a step-wise reconstruction of the input voltage.
Maybe another day I will describe the R/2R ladder, which is a more practical way to binarily weigh more than handful of bits.
LTSPICE is a valuable tool set, and is available at no cost, so don't let the price stop you.
Download this LTSPICE model at: https://lawsonlabs.com/SPICE_sar/SAR4.asc
In SPICE you can add bits of resolution without worrying about the noise floor. You can speed up the conversion without much regard for the realities of slew rates and settling times. Maybe best of all, you can experiment without worrying about producing a cloud of bad-smelling smoke that lingers in the air. If you do want to build this sort of converter, that would be a different exercise, but the modeling here should give you a good grasp of the underlying methods.
Tom Lawson
March 1, 2021