04-27-2021, 06:49 PM
Ground loops are like gremlins that can plague your circuitry. Ground loops often behave unpredictably and can appear to come and go. They present one of the more challenging trouble-shooting tasks for precision instrumentation. Most discussions of ground loops focus on hum in audio systems. Usually, the ground loop is formed by redundant grounding through shielding and through the third prong of power plugs, with building wiring forming part of the loop. Because any loop is an antenna, and antennas pick up ambient noise, line frequency is then injected into audio signals. We know that problem as hum. The amplitude and frequency of noise pickup in a loop depends on the loop area and geometry as well as nearby sources of ambient noise. It is no wonder that the AC behavior of ground loops is hard to pinpoint.
Fortunately, the DC behavior is easier to understand and track down. When you eliminate DC ground loop errors you will probably solve any AC problems, as well. So here, we will focus on direct current. In lower resolution instrumentation, you can get away with a lot of sloppiness, and those habits die hard. A 12-bit A/D converter resolves one part in 4096. For a 10 volt range, that means one count is about 2.44 mv. If you have a 2.44 ma ground current flowing in a wire with 1 ohm of resistance, that will amount to one count on your A/D converter. An ohm is a fair amount of wire resistance. It takes almost 25 feet of 26 gauge copper wire to get an ohm of resistance. So, unless you are dealing with larger currents or longer wires, in a 12-bit system, you can generally ignore the interconnection resistance, and think of wires as ideal conductors.
That is not so in high resolution systems. A 24-bit A/D resolves to better than a microvolt on a 10 volt range. That means that milliohms of resistance show up in your voltage data when milliamps of current flow. Whenever any current is flowing, connecting two points with a wire does not mean that the two points are at the same DC potential. That truth is counterintuitive. The fiction of equi-potential connections obscures the source of many grounding problems.
Further, in practical systems, loads are switched on and off. Valves, fans, heaters, motors or pumps cycle as an instrument operates or a process proceeds. Those switched loads involve more than enough current to alter the relative “ground” potentials in a system. Those changes interact with the geometry of interconnection to change where currents flow. If ground loops are present, seemingly mysterious behavior is not unexpected. Here is a simple example simulated in LTSpice.
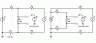
Start with a switched load and some control circuitry shown as a dotted box. On the left, the power supply connections are daisy-chained. On the right, each circuit has its own connections back to the 10 volt power source. The wires are shown as 1 ohm resistors and the switched load is one amp. Yes, that may be a bit strong, but the effect here is volts, so if your currents are milliamps instead of amps, the effect will still be millivolts.

The upper trace shows 2 volts of interaction in the difference between the V1 and V2 terminals of the control circuit, which is illustrated here as a dotted box. That large change is the result of the two one ohm resistors in series with the one amp switched current. The lower trace shows 2 to 3mv of non-ideality. The 1 mv step is seen because the voltage source is not perfect. (Like zero resistance wire, perfect voltage sources are hard to obtain in the field.) This voltage source has a one milliohm of source impedance, causing a 1 mv change with the one amp load step. Then, because the 10K resistor in the dotted box draws essentially one milliamp from the 10 volt source, each of the other two 1 ohm resistors have a one millivolt drop across them. Even so, the difference between the properly wired right-hand circuit is three orders of magnitude better than the left-hand circuit.
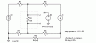
Now, we can insert a ground loop. The ground loop is represented by the new resistor in the center bottom. To make the effect dynamic, the resistance is calculated, as the variable {rx}. The .step function increases the resistance from 1 ohm to 1.2 ohms in 200 milliohm increments with a different color trace for each. That resistance change is to represent the tempco of copper. (More on that below.) Because the new current path of the ground loop partially bypasses the original current return path for the switched load, the interaction with the differential voltage, Dif, is altered as seen in the resulting waveforms. The lower waveform is the same as the one above, but with the vertical scale magnified. Note that the DC interaction only occurs when the load is on.

It might seem that the interaction is reduced, but remember that the ground loop can come and go erratically. Further, when copper wire heats, its resistance goes up. When current is flowing in the wrong path, the wire can heat quite a bit. I know I have melted through insulation of a misplaced ground wire on more than one occasion. Copper has a tempco of 0.4% per deg. C. Since it takes many dozens of degrees to melt the insulation off of wire, you see that the resistance can change quite a lot. As a result, excess current can heat up the ground loop path, increasing its resistance enough to incline the current to find an alternate route. Different size wires will heat at different rates, so currents in different paths can be changing when it might seem that conditions should be static. Then, loads turn off or on, and the situation changes again. Think of multiple loads and loops and multiple warming and cooling wiring paths all interacting in indeterminate fashion. You would see slow thermal oscillations mixed with other DC effects. It would be non-trivial to simulate all that, but it is not hard to imagine.
Further, the switched load that alters the ground currents doesn't even have to be in your system. It could be elsewhere in the building, but plugged into the same AC branch circuit. There may be one earth ground for an entire building, so currents there can interact in more seemingly mysterious ways. Ground loop problems can come and go with the time of day or the season, following the building's HVAC system, or lighting requirements.
When you factor back in the AC effects, it is no surprise that the gremlins can appear to be in control. Your defense is proper wiring practice. It might seem like unnecessary extra bother to pay proper attention to system wiring, but that is the influence of the gremlin on your shoulder whispering bad advice in your ear.
Tom Lawson
April 26, 2021
Fortunately, the DC behavior is easier to understand and track down. When you eliminate DC ground loop errors you will probably solve any AC problems, as well. So here, we will focus on direct current. In lower resolution instrumentation, you can get away with a lot of sloppiness, and those habits die hard. A 12-bit A/D converter resolves one part in 4096. For a 10 volt range, that means one count is about 2.44 mv. If you have a 2.44 ma ground current flowing in a wire with 1 ohm of resistance, that will amount to one count on your A/D converter. An ohm is a fair amount of wire resistance. It takes almost 25 feet of 26 gauge copper wire to get an ohm of resistance. So, unless you are dealing with larger currents or longer wires, in a 12-bit system, you can generally ignore the interconnection resistance, and think of wires as ideal conductors.
That is not so in high resolution systems. A 24-bit A/D resolves to better than a microvolt on a 10 volt range. That means that milliohms of resistance show up in your voltage data when milliamps of current flow. Whenever any current is flowing, connecting two points with a wire does not mean that the two points are at the same DC potential. That truth is counterintuitive. The fiction of equi-potential connections obscures the source of many grounding problems.
Further, in practical systems, loads are switched on and off. Valves, fans, heaters, motors or pumps cycle as an instrument operates or a process proceeds. Those switched loads involve more than enough current to alter the relative “ground” potentials in a system. Those changes interact with the geometry of interconnection to change where currents flow. If ground loops are present, seemingly mysterious behavior is not unexpected. Here is a simple example simulated in LTSpice.
Start with a switched load and some control circuitry shown as a dotted box. On the left, the power supply connections are daisy-chained. On the right, each circuit has its own connections back to the 10 volt power source. The wires are shown as 1 ohm resistors and the switched load is one amp. Yes, that may be a bit strong, but the effect here is volts, so if your currents are milliamps instead of amps, the effect will still be millivolts.
The upper trace shows 2 volts of interaction in the difference between the V1 and V2 terminals of the control circuit, which is illustrated here as a dotted box. That large change is the result of the two one ohm resistors in series with the one amp switched current. The lower trace shows 2 to 3mv of non-ideality. The 1 mv step is seen because the voltage source is not perfect. (Like zero resistance wire, perfect voltage sources are hard to obtain in the field.) This voltage source has a one milliohm of source impedance, causing a 1 mv change with the one amp load step. Then, because the 10K resistor in the dotted box draws essentially one milliamp from the 10 volt source, each of the other two 1 ohm resistors have a one millivolt drop across them. Even so, the difference between the properly wired right-hand circuit is three orders of magnitude better than the left-hand circuit.
Now, we can insert a ground loop. The ground loop is represented by the new resistor in the center bottom. To make the effect dynamic, the resistance is calculated, as the variable {rx}. The .step function increases the resistance from 1 ohm to 1.2 ohms in 200 milliohm increments with a different color trace for each. That resistance change is to represent the tempco of copper. (More on that below.) Because the new current path of the ground loop partially bypasses the original current return path for the switched load, the interaction with the differential voltage, Dif, is altered as seen in the resulting waveforms. The lower waveform is the same as the one above, but with the vertical scale magnified. Note that the DC interaction only occurs when the load is on.
It might seem that the interaction is reduced, but remember that the ground loop can come and go erratically. Further, when copper wire heats, its resistance goes up. When current is flowing in the wrong path, the wire can heat quite a bit. I know I have melted through insulation of a misplaced ground wire on more than one occasion. Copper has a tempco of 0.4% per deg. C. Since it takes many dozens of degrees to melt the insulation off of wire, you see that the resistance can change quite a lot. As a result, excess current can heat up the ground loop path, increasing its resistance enough to incline the current to find an alternate route. Different size wires will heat at different rates, so currents in different paths can be changing when it might seem that conditions should be static. Then, loads turn off or on, and the situation changes again. Think of multiple loads and loops and multiple warming and cooling wiring paths all interacting in indeterminate fashion. You would see slow thermal oscillations mixed with other DC effects. It would be non-trivial to simulate all that, but it is not hard to imagine.
Further, the switched load that alters the ground currents doesn't even have to be in your system. It could be elsewhere in the building, but plugged into the same AC branch circuit. There may be one earth ground for an entire building, so currents there can interact in more seemingly mysterious ways. Ground loop problems can come and go with the time of day or the season, following the building's HVAC system, or lighting requirements.
When you factor back in the AC effects, it is no surprise that the gremlins can appear to be in control. Your defense is proper wiring practice. It might seem like unnecessary extra bother to pay proper attention to system wiring, but that is the influence of the gremlin on your shoulder whispering bad advice in your ear.
Tom Lawson
April 26, 2021