06-10-2021, 08:46 PM
In part 1 we covered simple logic and set/reset flipflops. Here I will show a simulation of a type D edge triggered flipflop.
First, why is edge triggering important? The reality is that when you create logic circuits to perform digital functions, they behave well, but can never be ideal. It will always take a finite of time to slew between logic levels, so state changes are not instant. The delay between the input and output of a simple logic gate is called a propagation delay. For a simple inverter, we say there is a propagation delay between the input switching and the output switching. The length of a propagation delay depends on the logic family, and also somewhat on the power supply voltage and the temperature and the loading, etc. For our purposes, the exact time delay is not important. What counts is that we wait long enough for all interdependent logic circuits to react to an input change before we rely on all the logic levels to be valid for the new conditions.
The easiest and most common way to insure that coherence is clocking. If the state of the system only updates at a sufficient fixed interval, all the ones and zeros should be comfortably at their correct levels at every clock time. When we say the system clock for the original IBM PC was 4.77 MHz, that is what we are referring to. The IBM PC microprocessor updated its state at that fixed, clocked rate.
So how does one add a clock input to a set/reset flipflop? As with most any digital logic task, there are multiple solutions. Here we will look at the internals of the 74LS74, a standard logic chip which includes two type D flipflops. Below is the diagram for one flipflop. The connection from Q bar back to the data input is a external connection, and is not part of the chip.

On the right is a flipflop very much like the standard RS flopflop discussed last time. The gates are three input NAND gates. The extra input on both the set and reset side allows the needed extra control to be added. Two other identical flipflops sit on the left. One follows new inputs called data and clock, and the other tracks the set and reset inputs that match up with equivalent inputs on the simpler flipflop form. The data appears at the Q and Q bar outputs when the low-to-high clock transition occurs. So a D-type flipflop has four inputs - set, reset, data, and clock. It has two outputs - Q and Q bar, although either of those can be omitted to save a pin on the package.
The extra inputs on the three flipflops connect in non-obvious ways. Set and reset connect to the right-hand flipflop as before, so they act immediately, overriding anything that happens at the clock and data inputs. Reset also resets the clock/data flipflop. In the absence of active set or reset signals, the level at the data input is stored in the main latch when the clock transitions from low to high. That is accomplished by steering the clock signal to either the set or reset side of the main flipflop dependent on the state of the data input. Setting a flipflop that is already set changes nothing, just as resetting a flipflop that is already reset changes nothing.
There is an odd state where both Q and Q bar are high at the same time. That happens in this circuit whenever both set and reset are applied simultaneously. You might think that must be an error, but that anomolous state is part of the normal functioning of this type D circuit, making the analysis more challenging. The existence of a third state in a latch intended to hold one binary bit is counter-intuitive, but transitioning through that extra state is part of the edge-trigger mechanism here.
Understanding the internal details is a valuable exercise, but even more valuable is the ability to package the functionality, symbolize it, and use it according to the abstracted logical rules that apply. By abstracting functions that are more and more complex, you can build a digital system that is vastly more complicated than anything that a person could comprehend all at once.

The waveforms show how a D flop performs when you connect the Q bar output to the data input. It divides by two. Why? Because the data that is clocked into the latch is the data from the previous clock edge, but inverted. So, a clock when Q is zero and Q bar is one causes Q bar to be stored in the latch at Q, causing Q bar to become zero, etc. At first, it may feel circular and iffy, but once you get used to it, you will see that the divide by two function is basically bulletproof. In the waveforms you see a first period when reset is active (low), causing Q to stay low regardless. Then, for 4 tenths of a second the clock is divided by two. Finally, set is asserted (again active low), holding Q at one.
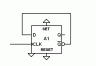
So now, if not before, when you see this symbol, you will see “divide by two”. All that complexity has melted away.
There are many on-line sources of information on the functioning of digital logic. I encourage you to explore them. Going forward, I will aim to focus on how the pieces fit together, and why it matters.
Tom Lawson
June 2021
First, why is edge triggering important? The reality is that when you create logic circuits to perform digital functions, they behave well, but can never be ideal. It will always take a finite of time to slew between logic levels, so state changes are not instant. The delay between the input and output of a simple logic gate is called a propagation delay. For a simple inverter, we say there is a propagation delay between the input switching and the output switching. The length of a propagation delay depends on the logic family, and also somewhat on the power supply voltage and the temperature and the loading, etc. For our purposes, the exact time delay is not important. What counts is that we wait long enough for all interdependent logic circuits to react to an input change before we rely on all the logic levels to be valid for the new conditions.
The easiest and most common way to insure that coherence is clocking. If the state of the system only updates at a sufficient fixed interval, all the ones and zeros should be comfortably at their correct levels at every clock time. When we say the system clock for the original IBM PC was 4.77 MHz, that is what we are referring to. The IBM PC microprocessor updated its state at that fixed, clocked rate.
So how does one add a clock input to a set/reset flipflop? As with most any digital logic task, there are multiple solutions. Here we will look at the internals of the 74LS74, a standard logic chip which includes two type D flipflops. Below is the diagram for one flipflop. The connection from Q bar back to the data input is a external connection, and is not part of the chip.
On the right is a flipflop very much like the standard RS flopflop discussed last time. The gates are three input NAND gates. The extra input on both the set and reset side allows the needed extra control to be added. Two other identical flipflops sit on the left. One follows new inputs called data and clock, and the other tracks the set and reset inputs that match up with equivalent inputs on the simpler flipflop form. The data appears at the Q and Q bar outputs when the low-to-high clock transition occurs. So a D-type flipflop has four inputs - set, reset, data, and clock. It has two outputs - Q and Q bar, although either of those can be omitted to save a pin on the package.
The extra inputs on the three flipflops connect in non-obvious ways. Set and reset connect to the right-hand flipflop as before, so they act immediately, overriding anything that happens at the clock and data inputs. Reset also resets the clock/data flipflop. In the absence of active set or reset signals, the level at the data input is stored in the main latch when the clock transitions from low to high. That is accomplished by steering the clock signal to either the set or reset side of the main flipflop dependent on the state of the data input. Setting a flipflop that is already set changes nothing, just as resetting a flipflop that is already reset changes nothing.
There is an odd state where both Q and Q bar are high at the same time. That happens in this circuit whenever both set and reset are applied simultaneously. You might think that must be an error, but that anomolous state is part of the normal functioning of this type D circuit, making the analysis more challenging. The existence of a third state in a latch intended to hold one binary bit is counter-intuitive, but transitioning through that extra state is part of the edge-trigger mechanism here.
Understanding the internal details is a valuable exercise, but even more valuable is the ability to package the functionality, symbolize it, and use it according to the abstracted logical rules that apply. By abstracting functions that are more and more complex, you can build a digital system that is vastly more complicated than anything that a person could comprehend all at once.
The waveforms show how a D flop performs when you connect the Q bar output to the data input. It divides by two. Why? Because the data that is clocked into the latch is the data from the previous clock edge, but inverted. So, a clock when Q is zero and Q bar is one causes Q bar to be stored in the latch at Q, causing Q bar to become zero, etc. At first, it may feel circular and iffy, but once you get used to it, you will see that the divide by two function is basically bulletproof. In the waveforms you see a first period when reset is active (low), causing Q to stay low regardless. Then, for 4 tenths of a second the clock is divided by two. Finally, set is asserted (again active low), holding Q at one.
So now, if not before, when you see this symbol, you will see “divide by two”. All that complexity has melted away.
There are many on-line sources of information on the functioning of digital logic. I encourage you to explore them. Going forward, I will aim to focus on how the pieces fit together, and why it matters.
Tom Lawson
June 2021