10-02-2020, 04:07 PM
The Model 203 and Model 333 are Delta Sigma converters built from discrete parts. First, why would we bother to do that? Back
during a boom period in the 90's I tried to order Delta Sigma converter chips from one of the major manufacturers. They said the
lead time was one year. I said yikes! Please place my order. They said, sorry, our system only goes out to 364 days, we can't
accept an order.
So, we designed and built the Model 203, a Delta Sigma converter that uses only ordinary, available parts. It has an RS-232
interface. A few years later, we added the Model 333, which is similar, but with a USB interface. The heart of a Delta Sigma A/D
converter is a modulator. A simplified SPICE version of the modulator is shown as Fig 1. The clock is in the lower left. It runs at 10
MHz. The analog input is at the upper left. In the center is a D-type flip/flop paced by the clock. The data to the flip/flop is the output
of a comparator that looks at whether the summing junction is above or below zero volts.
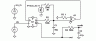
The summing junction is the combination of two signals, filtered together by series resistors and capacitor C1. The upper signal is
the analog input voltage, offset by -5 volts. The lower signal is the output of the flip/flop. The purpose here is to match the average
output of the flip/flop to the input voltage. In SPICE, logic signals can be ideal. In reality, the flip/flop output must be buffered to
produce a near-ideal logic 1 (5 volts) or logic 0 (0 volts). If the summing junction is positive, the data is a one. If it is negative, the
data is a zero. The result is a continuous string of ones and zeros at the point labeled Out. These are counted and filtered digitally
to obtain the conversion results.
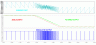
In Fig 2 that data Out is seen on the lower axis, labelled Modulator Output. The analog input, in red in the middle, starts at just
below the maximum value, then slews rapidly to just above the minimum value. Notice that the output data is almost always high at
first, and almost always low after the transition. The summing point is shown as the top trace. You can see that the 25us transition
period gives the system a little trouble. It can't quite keep up, so the summing junction jumps around showing a little sub-harmonic
behavior. That is not really a problem in a DC sense, because any errors get fed back and cancelled out.
The green trace is a filtered version of the output signal. It is not needed, and is not actually part of a Model 203 or 333, but it
does illustrate the validity of the modulator. Notice that during the rapid slew, the green trace does not perfectly follow the input
trace, even after allowing for the slight filter delay. That non-ideality shows the limits of the AC, or dynamic, reponse of this
particular Delta Sigma modulator. In practice, this circuit gives 20-bit performance for low frequency signals, and its frequency
response is set up to cut off sharply at 60 Hz. In Europe, a software constant is changed to move the cutoff to 50 Hz.
The simulation is a big help for understanding and design, but simulating the parasitics and other stray effects is as much an art as
a science. At some point, you need to move to the bench.
Tom Lawson
October 2020
during a boom period in the 90's I tried to order Delta Sigma converter chips from one of the major manufacturers. They said the
lead time was one year. I said yikes! Please place my order. They said, sorry, our system only goes out to 364 days, we can't
accept an order.
So, we designed and built the Model 203, a Delta Sigma converter that uses only ordinary, available parts. It has an RS-232
interface. A few years later, we added the Model 333, which is similar, but with a USB interface. The heart of a Delta Sigma A/D
converter is a modulator. A simplified SPICE version of the modulator is shown as Fig 1. The clock is in the lower left. It runs at 10
MHz. The analog input is at the upper left. In the center is a D-type flip/flop paced by the clock. The data to the flip/flop is the output
of a comparator that looks at whether the summing junction is above or below zero volts.
The summing junction is the combination of two signals, filtered together by series resistors and capacitor C1. The upper signal is
the analog input voltage, offset by -5 volts. The lower signal is the output of the flip/flop. The purpose here is to match the average
output of the flip/flop to the input voltage. In SPICE, logic signals can be ideal. In reality, the flip/flop output must be buffered to
produce a near-ideal logic 1 (5 volts) or logic 0 (0 volts). If the summing junction is positive, the data is a one. If it is negative, the
data is a zero. The result is a continuous string of ones and zeros at the point labeled Out. These are counted and filtered digitally
to obtain the conversion results.
In Fig 2 that data Out is seen on the lower axis, labelled Modulator Output. The analog input, in red in the middle, starts at just
below the maximum value, then slews rapidly to just above the minimum value. Notice that the output data is almost always high at
first, and almost always low after the transition. The summing point is shown as the top trace. You can see that the 25us transition
period gives the system a little trouble. It can't quite keep up, so the summing junction jumps around showing a little sub-harmonic
behavior. That is not really a problem in a DC sense, because any errors get fed back and cancelled out.
The green trace is a filtered version of the output signal. It is not needed, and is not actually part of a Model 203 or 333, but it
does illustrate the validity of the modulator. Notice that during the rapid slew, the green trace does not perfectly follow the input
trace, even after allowing for the slight filter delay. That non-ideality shows the limits of the AC, or dynamic, reponse of this
particular Delta Sigma modulator. In practice, this circuit gives 20-bit performance for low frequency signals, and its frequency
response is set up to cut off sharply at 60 Hz. In Europe, a software constant is changed to move the cutoff to 50 Hz.
The simulation is a big help for understanding and design, but simulating the parasitics and other stray effects is as much an art as
a science. At some point, you need to move to the bench.
Tom Lawson
October 2020