| Welcome, Guest |
You have to register before you can post on our site.
|
| Online Users |
There are currently 9 online users.
» 1 Member(s) | 8 Guest(s)
maximllles
|
| Latest Threads |
Thoughts on Obsolescence,...
Forum: Start Here
Last Post: HerbertDaf
09-05-2022, 04:55 PM
» Replies: 1
» Views: 10,123
|
A Brief Exploration of Bo...
Forum: Start Here
Last Post: Tom
04-05-2022, 04:10 PM
» Replies: 0
» Views: 2,484
|
The Fundamentals of Digit...
Forum: Start Here
Last Post: Tom
03-17-2022, 04:34 PM
» Replies: 1
» Views: 3,578
|
The Fundamentals of Digit...
Forum: Start Here
Last Post: Tom
03-15-2022, 08:32 PM
» Replies: 0
» Views: 2,490
|
The Fundamentals of Digit...
Forum: Start Here
Last Post: Tom
03-14-2022, 05:39 PM
» Replies: 0
» Views: 3,047
|
The Fundamentals of Digit...
Forum: Start Here
Last Post: Tom
03-10-2022, 07:23 PM
» Replies: 0
» Views: 2,228
|
Fundamentals of Digital E...
Forum: Start Here
Last Post: womantops660
03-10-2022, 07:29 AM
» Replies: 1
» Views: 3,248
|
What Does It Take to Get ...
Forum: Start Here
Last Post: Tom
02-21-2022, 04:36 PM
» Replies: 0
» Views: 2,530
|
Some History of Loop Cont...
Forum: Start Here
Last Post: Tom
12-24-2021, 02:49 PM
» Replies: 0
» Views: 2,304
|
Some History of Loop Cont...
Forum: Start Here
Last Post: Tom
12-17-2021, 04:23 PM
» Replies: 0
» Views: 2,240
|
|
|
| How Many of Those 24 Bits are Real? |
|
Posted by: Tom - 06-14-2021, 05:10 PM - Forum: Start Here
- No Replies
|
 |
If your purpose is to extract the most resolution and accuracy and reliability out of a 24-bit A/D converter chip, it takes more than wiring up a few connections. Here we look at the Lawson Labs Model 201, and analyze the various design considerations that went into it. The Model 201 is a worthy choice for this exercise because it is still going strong, 29 years after its conception. Lawson Labs has a reputation for reducing a task to its simplest terms. You can hang an A/D chip on a microprocessor with just a few additional components. Why does the Model 201 have so many parts?
Analog inputs
24 bit A/D chips like the AD7712 have built in self-calibration circuitry, which we employ. However, the common mode rejection is not nearly good enough to take full advantage of the accuracy and resolution of the A/D converter, so we add an input amplifier with excellent common mode rejection. That amplifier adds its own offset and gain errors, so an additional active calibration mechanism needs to be provided in order to maintain the DC accuracy.
A multiplexer must be placed in front of the new amplifier in order to to be able to run calibration signals through it to the A/D. In the case of the Model 201, there is an 8-channel differential multiplexer with six channels for input and two channels for calibration. All six available inputs have series protection resistors. Those resistors mean we require higher input impedance for the amplifier in order to maintain full accuracy. That high impedance is desirable for other reasons, as well. So, more than a little additional circuitry has been added to the Model 201 to obtain excellent common mode rejection.
Power input and power supplies
Most of the “extra” parts on the Model 201 are related to power supply regulation and decoupling. The Model 201 is designed for maximum flexibility of power input. It can be run from a 12V battery, a 48 volt DC supply, or from a wall adapter. For battery operation, power consumption must be minimized. Lower power means less self-heating, which is also an advantage for DC accuracy. First the power input is protected against reverse connection. Then, it is protected against overvoltage. Then, a 5 volt standby supply is generated. This supply is always on to keep the microcontroller alive and checking for wake-up commands. Next, the raw power input is regulated at 12 volts. From that, a charge pump produces a -12 volt supply. The +/- 12volt supplies are thus regulated, but not precisely regulated. The +/- 12 volt supplies are switched on and off by the microcontroller. They do not operate when the Model 201 is asleep, saving power. When awake, to power the sensitive analog circuitry the +/- 12 volts is re-regulated to +/-7.5 volts. An precise analog 5 volt supply is also derived, using a precision 5 volt reference that runs from the +12 volt supply. There are two more reference supplies needed by the A/D converter in order to take full advantage of its dynamic range. Those are at +/- 2.5 volts. Finally, a precision 5 volt reference output is provided for off-board circuitry.
Lets count - rectified filtered raw input, 5 volt standby, + 12, -12, + 7.5, -7.5, two 5 volt references, analog 5 volt supply, digital 5 v supply, +2.5v, and -2.5. It adds up to 12 power supplies total. In addition, various connections to the supplies are decoupled from each other with small value series resistors and capacitor filters. A typical decoupling network might be a 10 ohm series resistor with a 10 uF and a 0.1 uF shunt capacitor. Just one decoupling network per power supply would add 36 components. In fact, there are more decoupling components than that.
How does one determine how many decoupling networks to include? It is largely a matter of trial and error. My process was to exercise the A/D under the most demanding dynamic conditions and looking for any interactions. One good test is to apply a square wave to one channel and look for crosstalk on other channels. Another is to add noise on the raw power input and to look for additional noise anywhere else in the circuitry. Loading the digital outputs, and turning them rapidly on and off together should not affect the data. If it does, there is more decoupling work to do to isolate the analog and digital sides of the interface.
Optical isolation
There are a few more power supply components on the Model 201 board, but the power for them comes from the host computer serial port. The RS232 provides plus and minus power to an interface chip which drives, and is driven by, the optocouplers for the serial interface. The reasons for needing this additional level of isolation are explained in detail in other posts on this discussion site. For now, just remember that isolation breaks ground loops.
Back to the analog side - overvoltage protection
Over enough time, all sorts of mishaps at the analog inputs are bound to occur. The easy way to protect the A/D chip is with clamp diodes to the supply rails. Clamp diodes can leak enough current to add measurable error to a high impedance input. Also, clamp diodes turn on incrementally over a range of voltage and may not save the A/D chip when the transient hits. A better clamp, for more reliability and best accuracy, requires a comparator and an analog switch to guarantee proper protective clamping. That circuitry adds another handful of components to the Model 201.
Programmable filter
Delta sigma converters are wonderfully effective at rejecting most frequencies of input noise. Still, for any given data rate, there are certain frequencies that elude the digital filtration. The solution to that problem is an analog low pass pre-filter that can remove the unwanted frequencies. Active filters introduce DC errors, so we avoid them. A simple one-pole RC filter will do the low pass job, but because the Model 201 is digitally programmable over a wide range of data rates, different filter constants are appropriate for different circumstances. So, the Model 201 has three programmable analog filter time constants. That added functionality involves adding a high-quality filter capacitor and a half dozen other parts.
The remaining components on the Model 201 board are for digital input and output, and for expansion. There is also optical isolation for the four expansion outputs, A through D. Count two crystals for clocks and one decoding chip and one latch to multiplex pins on the microcontroller itself.
That is everything. All those extra parts, you see, are there for a reason. If you leave any of them off, there is a price to be paid. Maybe that is why the Model 201 is still an active, desirable product 35 years later. If you just need a little more than 16-bits of real resolution, you can get away with lot, when starting with a 24-bit delta sigma A/D converter chip. But, if you want 22 or 23 bits of real, usable, reliable resolution, you need to do everything exactly right.
Tom Lawson
June 2021
|

|
|
| Fundamentals of Digital Electronics, Part 2 |
|
Posted by: Tom - 06-10-2021, 08:46 PM - Forum: Start Here
- No Replies
|
 |
In part 1 we covered simple logic and set/reset flipflops. Here I will show a simulation of a type D edge triggered flipflop.
First, why is edge triggering important? The reality is that when you create logic circuits to perform digital functions, they behave well, but can never be ideal. It will always take a finite of time to slew between logic levels, so state changes are not instant. The delay between the input and output of a simple logic gate is called a propagation delay. For a simple inverter, we say there is a propagation delay between the input switching and the output switching. The length of a propagation delay depends on the logic family, and also somewhat on the power supply voltage and the temperature and the loading, etc. For our purposes, the exact time delay is not important. What counts is that we wait long enough for all interdependent logic circuits to react to an input change before we rely on all the logic levels to be valid for the new conditions.
The easiest and most common way to insure that coherence is clocking. If the state of the system only updates at a sufficient fixed interval, all the ones and zeros should be comfortably at their correct levels at every clock time. When we say the system clock for the original IBM PC was 4.77 MHz, that is what we are referring to. The IBM PC microprocessor updated its state at that fixed, clocked rate.
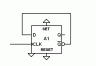
So how does one add a clock input to a set/reset flipflop? As with most any digital logic task, there are multiple solutions. Here we will look at the internals of the 74LS74, a standard logic chip which includes two type D flipflops. Below is the diagram for one flipflop. The connection from Q bar back to the data input is a external connection, and is not part of the chip.

On the right is a flipflop very much like the standard RS flopflop discussed last time. The gates are three input NAND gates. The extra input on both the set and reset side allows the needed extra control to be added. Two other identical flipflops sit on the left. One follows new inputs called data and clock, and the other tracks the set and reset inputs that match up with equivalent inputs on the simpler flipflop form. The data appears at the Q and Q bar outputs when the low-to-high clock transition occurs. So a D-type flipflop has four inputs - set, reset, data, and clock. It has two outputs - Q and Q bar, although either of those can be omitted to save a pin on the package.
The extra inputs on the three flipflops connect in non-obvious ways. Set and reset connect to the right-hand flipflop as before, so they act immediately, overriding anything that happens at the clock and data inputs. Reset also resets the clock/data flipflop. In the absence of active set or reset signals, the level at the data input is stored in the main latch when the clock transitions from low to high. That is accomplished by steering the clock signal to either the set or reset side of the main flipflop dependent on the state of the data input. Setting a flipflop that is already set changes nothing, just as resetting a flipflop that is already reset changes nothing.
There is an odd state where both Q and Q bar are high at the same time. That happens in this circuit whenever both set and reset are applied simultaneously. You might think that must be an error, but that anomolous state is part of the normal functioning of this type D circuit, making the analysis more challenging. The existence of a third state in a latch intended to hold one binary bit is counter-intuitive, but transitioning through that extra state is part of the edge-trigger mechanism here.
Understanding the internal details is a valuable exercise, but even more valuable is the ability to package the functionality, symbolize it, and use it according to the abstracted logical rules that apply. By abstracting functions that are more and more complex, you can build a digital system that is vastly more complicated than anything that a person could comprehend all at once.

The waveforms show how a D flop performs when you connect the Q bar output to the data input. It divides by two. Why? Because the data that is clocked into the latch is the data from the previous clock edge, but inverted. So, a clock when Q is zero and Q bar is one causes Q bar to be stored in the latch at Q, causing Q bar to become zero, etc. At first, it may feel circular and iffy, but once you get used to it, you will see that the divide by two function is basically bulletproof. In the waveforms you see a first period when reset is active (low), causing Q to stay low regardless. Then, for 4 tenths of a second the clock is divided by two. Finally, set is asserted (again active low), holding Q at one.
So now, if not before, when you see this symbol, you will see “divide by two”. All that complexity has melted away.
There are many on-line sources of information on the functioning of digital logic. I encourage you to explore them. Going forward, I will aim to focus on how the pieces fit together, and why it matters.
Tom Lawson
June 2021
|

|
|
| Fundamentals of Digital Electronics |
|
Posted by: Tom - 06-10-2021, 01:46 PM - Forum: Start Here
- Replies (1)
|
 |
Computers these days are so complex that a beginner could be excused for thinking that they could never begin to understand what makes them work. That was not true 55 years ago when I developed an interest in digital circuits. Previously, electronics had meant radio, and hobbyists had boxes of tubes stashed in their rooms and long antennas strung in their backyards. In 1966, few people had ever seen a computer or a calculator.
The central innovation of digital electronics was binary data. The function to be performed was expressed numerically, with numbers stored in binary form, meaning ones and zeros. Most computers used “core” memory to store digital information by polarizing ferrite magnets in one of two directions. Back then, the flip/flop was the next big thing. Using two transistors, which were newfangled semiconductor devices, you could build a circuit that had two stable states. The states were called set and reset, and a flip/flop required two inputs, one to set it and one to reset it. At any time, the flip/flop would be in one of those two states, set or reset, one or zero. Eight flip/flops could store an eight bit digital word, called a byte. If you knew that in 1966, you were definitely a nerd.
Back then, building a one byte memory was a big project. Just buying the 16 transistors required was a major investment for a student. We didn't see the microcomputer coming, but it was apparent that digital circuits could be put to many uses. Counters were cool, you could count up or down in binary. If you had an oscillator, you could count pulses and keep time. If you were going to put your flip/flops to work, a few additional fundamental logic elements would be needed. Those were the AND function, the OR function, and the NOT function. A NOT function is just an inversion. NOT turns a zero into a one and a one into a zero. It only takes one transistor to build the NOT function. You can make an OR circuit with two diodes (called a wire OR) or better, with two transistors. Actually with two transistors you would get a NOR function, that is to say NOT OR. A NOR gate with two inputs performs the logical function expressed in words as, if either input is a one, the output is a zero, otherwise, the output is a one. If you add a NOT after a NOR, that brings you back to OR, so you really need three transistors to make an OR function.
So, it was reasonable in the '60s to build AND, OR and NOT functions by hand, out of transistors. With just those building blocks, you could make a counter, or an adder, or a primitive calculator. It became a matter of scale. Now there are a billion transistors in an ordinary microprocessor that costs less than those 16 transistors cost in 1966. At that scale it is easy to forget that you can reinvent the whole universe of digital computing from AND, OR and NOT. To begin, here is a flip/flop built out of two transistors.

Both the stored value, usually called Q, and its inverse NOT Q, also called Q bar (shown as Q with a line over it), are available. Pressing the set button turns on transistor Q1 which pulls output Q bar to zero. With Q bar at zero, Q2 is turned off through R4. Output Q rises, due to the pull-up action of R1. Output Q then, through resistor R3, insures that Q1 stays on, which insures that Q bar stays at zero. So, the state of the flip/flop would stay set indefinitely. Pressing the set button again causes no change, but pressing reset reverses the process, causing Q to be stuck at zero and Q bar to be at 1. A flip/flop remembers one bit.

These days you can buy logic gates with one or two or four simple gates in a package, so next consider a flip/flop built out of two NOR gates. In a NOR flip/flop a logic one sets or resets the state. Logic zero at an input is ignored. Function is straight forward. Here are waveforms generated in LTSPICE.

If the last activity at the input was a set, the state of Q will be one. If the last input was a reset, the state of Q will be zero. The only ambiguity is if the flip/flop is set and reset at the same time the result will be indeterminate. In that situation, whichever input persists longer, set or reset, will determine the state that the flip/flop is left in. Additional logic can be added to cause deterministic behavior when set and reset act together. If you want set to override reset, you could gate the reset signal with an AND gate to block the reset signal when there is also a set signal. In words, resetout equals resetin AND NOT set. I hope you begin to get the picture.
There is one more ambiguity. When power is applied to a flip/flop circuit it may come up in either a set or reset condition. Good design always takes uncertain initial conditions into account. For example, the flip/flop might be reset by a reset signal OR by a power-on signal which is present only briefly. Then, resetout equals (resetin OR power-on) AND NOT set. The parenthesis indicate “do this first”. Maybe power-on should take precedence over set. Then, rearrange the order of the same elements to get resetout equals (resetin AND NOT set) OR power-on.
For completeness, you can also build a flop/flop built out of two NAND gates. In that case, a logic zero sets or resets. You might say that the NAND flip/flop inverts compared to a NOR flip/flop, but since both polarities, Q and Q bar, are available in both cases, it is a non-distinction.
Having explored the logic of set/reset flip/flops, a next step might be to explore how to add two binary numbers using flip/flops, AND, OR, and NOT, or it might be how to make a flip/flop that is edge-triggered, that is to say, it only updates its state when a clock signal transitions. A series of such small steps will get to latches and counters and encoders and decoders, and in fact, all logic functions, right up to the microprocessor.
Tom Lawson
June 2021
|

|
|
| Electrochemistry, and What in the World is an Ussing Chamber? |
|
Posted by: Tom - 06-07-2021, 01:48 PM - Forum: Start Here
- No Replies
|
 |
Electrochemistry, as apparent from the name, is the study at the margin between electricity and chemistry. Chemists consider electrochemistry to be a branch of chemistry, while engineers don't consider electrochemistry to be a branch of electronics. The resulting asymmetry complicates the situation for those few of us approaching electrochemistry from the electronics side. Electrochemical matters are viewed differently by normal folk who don't have Ohm's Law tattooed on their cortex. So here, we will look at an Ussing Chamber as an electrical apparatus, with chemistry somewhere in the distance, and with biology hovering at the far horizon. The ultimate object of taking a step back is to simplify, given the underlying principle.
If you remember anything from a physics or chemistry course, you will know that interactions between atoms and molecules are largely driven by electric charge. Electrons are mobile, negatively-charged particles that mix and match according to relatively simple rules, which soon lead to a huge variety of complex behaviors. For example, we know that when you combine oxygen and hydrogen and a spark you get explosive energy, plus a very little bit of water. There is no electrical circuit involved, and Ohm's Law does not seem at all relevant. Yet the reverse reaction shows a clearer picture. Hydrolysis is the running of an electric current, being a stream of charged particles, through ionized water and so producing oxygen at one electrode and hydrogen at the other. It is not that hard to measure the current and count the atoms and see that there is a simple, fixed relationship. That study is called coulometry, and it stands squarely at the intersection of chemistry and physics and electronics.
An Ussing Chamber is a particular apparatus for coulometry involving a membrane. Since membranes tend to fall in the purview of the life-sciences, we now need to add biology to the mix. The various skills required to master all of the above are becoming excessive. Let's make the electronics piece as simple as possible. Modern electronics with a computer overseeing a process can do things that were inconceivable when Hans Ussing invented the Ussing Chamber in 1946. If you accept his view of its experimental capabilities, you will sell it far short. Think of the modern electronic interface as an ideal view into the chamber's electric internals, without the compromises needed for 1940's technology.
An Ussing Chamber contains a conductive solution, or electrolyte, divided into halves by a membrane. There are two pairs of electrodes, each pair with one electrode on either side of the membrane. One pair of electrodes simply measures the voltage difference across the membrane. The other pair of electrodes injects a current, where ions must cross the membrane to complete the electric circuit. The object is to quantify an electrochemical reaction in terms of the relationship between voltage and current. You may be studying the membrane itself, or properties of the electrolyte, or of substances added. In any case, you don't want the voltage and current measurements to interact. To the extent you must draw current in order to measure voltage, that constitutes an error. If you cannot provide a particular current at a particular voltage, that is a real limitation. Currents and voltage differences can be very small, so resolution is at a premium. These reactions usually proceed slowly, so faster measurement speed is generally not required. Since it can take hours for these systems to reach equilibrium, long-term stability of the electronic interface is essential.
The relationship between voltage and current will reflect the chemistry. The modern apparatus can control either one, and measure the other in any sequence desired. For older technology, you would set a voltage which would result in a current flow. The amount of current flow corresponding to the voltage would depend on series resistance. (Remember Ohms Law?) Series resistance might be largely determined by electrode geometry or aging, or by temperature, or other incompletely controlled variables. More series resistance would need to be added in order to measure small currents. The modern apparatus can eliminate series resistance as an error term. If the current is set to 1 nA, it is 1 nA with an ohm of series resistance or a megohm of series resistance. You can sweep the relationship of voltage to current, or current to voltage, over a chosen range at a chosen rate in steps or with a smooth ramp. You can reverse polarity at will. Again, you can fix the current and measure the resulting voltage, or fix the voltage, and measure the resulting current.
The Lawson Labs Ussing Chamber interface uses Excel as the intelligence, so the user has complete control without needing to know a programming language. If you are familiar with Excel, you are halfway up the learning curve, already. There is no need to add electronics or programming to the list of skills required. That is good thing, because electrochemistry is complex enough to begin with.
Tom Lawson
June 2021
|

|
|
| Flash Memory and Cybercrime |
|
Posted by: Tom - 05-26-2021, 06:28 PM - Forum: Start Here
- Replies (2)
|
 |
Back in the halcyon days of computing, we had hardware, software, and in between, firmware. Firmware was the programmable aspect of the hardware. Originally, firmware instructions could be written once into programmable parts, and that was that. Programmable Read only Memory was known as PROM. According to Wikipedia, it was invented in the '50s, but it became important in the '70s as the repository of the permanent code for microprocessors. Masked ROM could be manufactured with the programming built in, but that involved big upfront expenses and long lead times. Masked ROM has always been the lowest cost firmware for high volume applications, but it is prohibitively expensive for other uses.
Erasable parts, called EPROMs also appeared in the 70's. These parts could be erased through a quartz window by UV light. Then, the same part could be reprogrammed to suit. To reprogram a part, it was first placed in an eraser, which included a strong UV source, and usually a timer. After many minutes (depending on the part and the intensity of the UV light), the memory would be checked to see if it was blank. If so, it was ready for reprogramming. Parts were capable of only a limited number of program/erase cycles, but the erasable technology made firmware development considerably less stressful. Still, there was a real premium on getting it right in the smallest number of iterations.
Prototype systems would be built with EPROM chips, but they were more expensive, and could lose their data over time. Production systems would use PROM or masked ROM for economy and reliability. This arrangement worked pretty well for a number of years. A PROM or ROM would hold the BIOS for your home computer and a keyboard PROM or ROM would hold the translation between keycodes and pixels for the alphanumeric display.
EEPROM, or Electrically Erasable Read Only Memory, was the next phase of development. Your USB memory stick is the modern form of this rather elegant technology. That USB stick uses flash memory, which is a form of EEPROM that was first commercialized in the '80s. Flash has been improved to the point that electrically erasable memory can replace a hard drive. That is a long way from 20 minutes in the UV eraser before rewriting.
When combined with internet accessibility, EEPROM memory enables field reprogrammability. Our computers are now almost all connected, and more and more of our infrastructure is network-connected, too. We have become accustomed to over-the-air firmware updates for our phones, computers, networking systems, etc. Those updates remove the need to complete product development before beginning production. Once you are close, you know you can fix it later, with an update. The developer can add features and fix bugs long after the product is shipped. The update process can be beneficial, but it is also corrosive. There is no longer a need to get it right the first time, or even the second time. In fact, the constant parade of patched problems has become a feature. It is called software as a service. The product is no longer an entity, it is a continually morphing work in progress.
In the above process, it has become more and more difficult to make the distinction between firmware and software. Maybe that distinction is becoming irrelevant, but the recent increase in the number of malicious hacks into supposedly secured systems makes me think otherwise. Mistakes find their way into the firmware that sits beneath the application code. That firmware is rarely examined. The deeper code is buried, the harder it is to sort out the rules and assumptions for its function. Code at the lower levels should be thoroughly debugged, tested and documented. Only then can it be safely forgotten. When a breach allows that underlying code to be exposed to hackers who can actually change it, good luck ever figuring out what went wrong after you have paid the ransom to recover your data.
Further, when bugs find their way into low-level code, they have a sneaky way of propagating. One of the early BASIC language implementations had a bug in the PEEK statement. PEEK was a command to read an 8-bit byte from a memory address. PEEK mistakenly treated the result as a signed 7-bit integer. Anything over 127 was shown as a negative number. That made a mess when reading A/D converter data. You might think a problem like that would be corrected promptly and permanently. In fact, that same problem turned up in several completely different versions of BASIC from different companies, even five years later. So when problems appear at the lowest levels of embedded code, watch for more trouble in the future. Thanks largely to flash memory, even the hackers don't know all the places their backdoor access may be installed.
Tom Lawson
May 2021
|

|
|
| Analog Outputs with Oomph |
|
Posted by: Tom - 05-17-2021, 08:20 PM - Forum: Start Here
- No Replies
|
 |
Here, we are moving on from buffered digital outputs to buffered analog outputs. Analog outputs require quite a bit more circuitry in order to provide the necessary power and reliability. Since analog outputs are often used to power heaters or motors or other controls within feedback loops, they should be monotonic. That means the output should always go up when instructed to increase, and go down when instructed to decrease. If there is a non-monotonic wrinkle in the response, the feedback loop will likely find it, and will tend to get stuck at that point, because non-monotonicity will cause positive feedback.
Proportional controls need to handle a wide range of supply voltages efficiently, and must survive the voltage and current spikes associated with switching inductive loads like valves, motors and many heaters. With precision analog circuitry physically near by, it is also critical that the proportional outputs not generate large amounts of electrical noise or too much heat. Purely analog proportional control involves dissipating a large amount of heat. That means switching techniques are usually preferred instead. Switched power, done right, can be very efficient, but care must be taken to limit radiated electrical noise. The list of requirements already goes far beyond that for the previously discussed digital outputs.
The voltage dropped across a bipolar transistor when turned all the way on causes a lot of heat at higher currents. That means the bipolar transistors we used in the previous digital output discussion are not best for analog outputs. Modern FETs are small and affordable, and they have tiny on resistances, measured in milliohms. That means they have very small voltage drops when on, even at higher currents, so they stay cool. The trick is to turn them on and off at a relatively fast rate, so that they appear to be in an intermediate steady state. That technique is called Pulse Width Modulation, or PWM. For example, if the FET Turns on and off for alternate equal periods, it will run the load at half the maximum current. With the frequency held constant, the on time, or pulse width, becomes the controlling factor.
Generally, you would prefer the switching frequency be outside of the audible range, or above 20 kHz (corresponding to a base period less than 50 us). If the FET takes very long to turn on or off, at 20 kHz it will spend a high percentage of the time partially on. That is not good for efficiency. The FET dissipates almost no power when it is all the way on, or all the off, but in between there is both current flow and substantial voltage across the switch. Volts times amps equals Watts, so the FET heats during the switching action. That inefficiency contributes to what is called switching loss. Faster control brings faster switching and lower losses.
Because it takes a certain minimum amount of time to turn a switch on, and again a minimum time to turn the switch off, you usually cannot have a super-small duty cycle, like a small fraction of one percent. If it takes at least 1 us to turn on and off, the minimum duty cycle at 20 kHz would be near 2%. The same applies at the other end of the scale. You can have a 100% duty cycle, but not 99.99% unless the base period for your PWM is impractically long.
As with higher current digital outputs, isolation is a good idea to separate high current paths from sensitive analog circuitry. As in the digital case, an optocoupler is the usual isolation means. Conveniently, because the FET is either on or off, a single bit of digital information serves to isolate a PWM analog output, but one issue quickly shows itself. Optocouplers are slow switching devices. You can't just run a FET from an optocoupler without having the switching losses go through the roof. The optocoupler output has to be the input for a circuit that pulls the gate of the FET up or down hard and fast. In order to rapidly slew the capacitance of the gate, a rather high peak current is required. So, to switch efficiently, you need to pull up or down fast, but not both at same time, and you need to be sure you don't let the gate of the FET spend any time in an indeterminate state. If the FET is left half on, half off, it will self-destruct before you can reach the power switch.
When you have optical isolation, you need a separate power supply on the isolated side. For these proportional output circuits, the isolated side power supply could be 48 volts or 8 volts, or anything in between. Different power FETs have different gate drive requirements, but all perform best when the gate voltage is switching between particular levels. That means you need the regulate that 8 to 48 volts to produce the desired gate drive voltages. All around, those driver circuits need careful attention. Don't try them at home without some prior experience with simpler interfacing.
The Lawson Labs PDr4 is just such a device. It includes a PWM interface to turn a low current analog input voltage into a PWM duty cycle, an optocoupler for isolation, a regulator to power the isolated side, and a snappy, beefy buffer optimized to take in the optocoupler signal and turn it into gate drive to the power FET. The PDr4 has two other necessary, but non-obvious features. First, it includes a clamp diode to keep the switched output point from rising much above the power supply voltage. To the extent that a switched load is inductive, the switched point will spike up to a higher voltage when the switch is opened. (Think of the need for a suppression diode on a relay coil.) The clamp diode conducts that energy, preventing damage from overvoltage.
The other feature is thermal protection. No matter how capable an output driver may be, there will always be a case where it is pushed beyond its ultimate limits. Thermal shutdown turns the switch off before it gets too hot. You need to be a bit careful how that is done. If the thermal limit causes the FET switch to turn off only momentarily, it will cool a bit, then turn back on again right away. Additional rapid turning off and on when near the temperature limit could destroy the FET. Instead, when the temperature limit is hit, the PDr4 stays off untill it has cooled to well below the upper limit. Then it snaps back to normal operation.
For lower proportional output currents we offer expansion boards with one, two or three isolated proportional drive circuits. (You might have to ask for details.) Those analog drivers are similar to the PDr4 circuits, but with lower voltage and current ratings. So why go to all the extra trouble for proportional control compared to just turning, say, a heater, on and off to control a temperature? You are bound to alternately overshoot and undershoot using that method, plus the timing of the on/off switching becomes critical. If instead, you set a proportional control to nearly match the required heating in a steady state condition, ocassional fine tuning the heater current at non-critical intervals will keep the temperature very near where you want it to be.
Tom Lawson
May 2021
|

|
|
| Optical isolation - Gremlin's Nemisis |
|
Posted by: Tom - 05-05-2021, 04:25 PM - Forum: Start Here
- No Replies
|
 |
If you have looked at the ground loops discussion and the simple digital output description you have all the background you need to appreciate why an optocoupler on a digital output can help keep the gremlins at bay. Start from the basic buffered digital output circuit which uses a single transistor to switch amps of current under the control of a logic-level digital output.
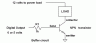
That digital output signal is generated from the logic power supply in the data acquisition system. That means it is referred to the power ground at the data system. The emitter of the power transistor in the figure is referred to that same ground. It has to be, in order for the digital output signal attached to the base to correctly turn the transistor on and off. That means the high current passed by the buffer transistor needs to flow in a connection to the same ground as the data system ground. As described in the section on grounding and ground loops, that can be done best by providing a separate conductor to carry the large current.
Still, there is a possible problem lurking here. Lets say you have a 24 volt power suppy powering the load at the digital output buffer. That 24 volt supply may also run other elements in your system, perhaps a motor, a fan, or a heater. Those higher current loads must also be referred back to the 24 volt power supply ground, which is now the same as the logic supply ground. The plain mechanics of connecting many high current, (that is to say larger diameter,) wires to a single-point ground quickly become awkward. Also, the electric fields generated by the wires carrying the high load currents then would necessarily be physically closer to the sensitive data system. Remembering that such fields interact in proportion to the square of the distance, a little extra separation goes a long way. We would rather be able to separate the high current loads both electrically and physically from the analog inputs and controls. Fortunately, there is an easy way to isolate a digital output signal by using light to carry the information across an isolation barrier. A class of components called optocouplers perform that function. A light-emitting diode (LED) shines on a phototransistor. Without a direct electrical connection, the diode can turn the phototransistor on or off. There is a lot to know about optocouplers, but for this simple application the smallest, cheapest, most common sort of optocoupler is fine for the job. We'll use a 817 type optocoupler, which is a 4-pin device.

The digital output itself now needs only to turn on or off the LED inside the optocoupler. The phototransistor then provides the base current needed to turn on the buffer transistor. The optocoupler won't reliably provide a lot of current, so we generally use a Darlington for the power stage. That way, we won't be limited by the optocoupler current transfer ratio or by the buffer transistor current gain. The resistor R1 sets the LED current, and the resistor R2 limits the transistor base current. If you know the base current will stay in the safe zone for your buffer transistor, as limited by the optocoupler, you can omit R2.
Now, the higher power circuitry associated with the digital load is completely separate from the powering of the data system. That frees up the geometry of your system so that you can arrange the various elements for convenience, instead for minimizing loop area and radiated energy. With individually isolated digital outputs, different loads could even run from different power supplies. You would be unconstrained. Note that you may want to reconnect the grounds that we have just disconnected when we added the optocoupler. No, that would not make the whole exercise futile. With isolation, you get to make a low-current ground connection, and in the most favorable location. That is a big difference. To visualize, think of two star ground points, one for grounding noisy, high current loads and one for quiet low current power and signal grounds. Adding the optocoupler allows you to physically and electrically separate those two star grounds, and, if you choose, to connect them together with a low-current, gremlin-free, conductor.
We still didn't address using FETs for buffering digital outputs. Please check back later.
Tom Lawson
May 2021
|

|
|
| Digital Outputs are Dead Simple, Right? |
|
Posted by: Tom - 05-04-2021, 01:52 PM - Forum: Start Here
- No Replies
|
 |
One of the simplest elements in a data acquisition and control system is a digital output. Its state is either ON or OFF. What could be simpler than that? If the output comes from a logic chip, the exact properties will depend on the logic family and the power supply voltage for the logic chip. Those details are the stuff of data sheets, but are not our focus here. You can count on a few things, regardless. The digital output will either be near the logic power supply voltage or near ground, corresponding to a logical one or a logical zero, on or off. The current available to drive the digital load will be a few mA, more or less. If you need, say, 25 mA of drive current, you need help in the form of a digital buffer. A buffer provides the same one or zero output, but at higher current, and possibly at a higher voltage as well. The amount of help needed depends on how much drive current is required. Up to a few hundred milliamps, a small one-transistor buffer will do the job. Up to a few amps, a big transistor is called for. For higher power loads, you are looking at a relay, or a solid-state output module, or a more sophisticated buffer, probably using a FET switch. A big relay needs more than a few milliamps to drive it, so you may have a two-stage interface involving a small buffer to drive a big relay. For AC loads powered from a wall outlet, you will need isolation for safety. Here, we will limit ourselves to lower voltage DC loads.
A single transistor can handle most of these cases. A transistor used as a switch takes in a small current and turns it into a much larger current. That is called current gain. A transistor might have a current gain of 50, so that 2 mA of drive could provide 100 mA of load current. For extreme current gain you will use two transistors together in a single package called a Darlington, but from the outside, it looks the same as a single transistor. Without going into what, exactly, a transistor is, lets stick to a simple functional description of an NPN transistor. It has three terminals labeled collector, base and emitter. When voltage is applied to the base, current flows from collector to emitter. The collector emitter current can be much higher than the base current.

First, select a transistor for the buffer that can handle the current you need. Next, consider the voltage. Your digital output is probably 0 or 5 volts, but your load might require 12 or 24 volts. That is not a problem. Almost any transistor will handle those sorts of voltages. The collector voltage can be lots higher than the base voltage, up to the rating of the transistor. The base voltage, however, will be limited to about 0.6 volts above the emitter voltage by the intrinsic diode represented by the arrow on the emitter. For that reason, you will put a resistor in series with the base of the transistor buffer. The resistor will establish the base current.
Transistors have specifications for maximum base current. You don't want or need to approach those limits. You just need sufficient base current to insure that the transistor is turned on strongly enough to pass the necessary load current. As in the example above, say your transistor guarantees a current gain of times 50, and you need 100 mA to drive your load, so you need at least 2 mA of base drive. If the digital output voltage when loaded is at least 4.6 volts, and the base of the transistor when on is at 0.6 volts, there will be a 4 volt drop across the base resistor. Using Ohm's law, 4 volts / 0.002 amps yields a resistor value of 2 K ohms. It is fine to use less resistance. You want the buffer to turn on vigorously and excess base current is not a problem so long as you avoid approaching the maximum allowed.
In case the above was too much detail, just think of the transistor as a switch. Zero volts is off, and something above 0.6 volts is on. Before building your buffer, there is one more thing that needs to be considered. Will it get too hot? The transistor has a power dissipation rating that should not be exceeded. The wattage dissipated by the buffer depends on the voltage drop across the transistor when it is turned on. The transistor specifications will show a saturation voltage, which is the voltage across the transistor when it is turned all the way on. The saturation voltage goes up with the current, so keep on the conservative side. Say that number is 0.5 volts. Power is voltage times current, so 0.5 volts * 0.1 amps equals 0.05 watts. The small through-hole transistor package is always good for 1/4 watt, so everything looks good. For those loads of around 100 ma, common transistor types 2N3904 or PN2222 will be fine up to 50 volts. For more than a few hundred mA, you will want a transistor in a larger package. Usually that would be a TO-220 package instead of a TO-92 package. You may pick something like a TIP41C in a TO-220 package, which handles many watts at up to 100 volts. The TIP41C might have 1.5 volts across it when turned on, but it can handle a lot of power. It does have more limited current gain than the smaller transistors, with a minimum gain of times 15. If you need more than that, the aforementioned Darlington is your buffer. The TIP112 has a current gain of over 1000, so that won't be what limits you.
To summarize, pick a buffer transistor that will handle the current and voltage and power needed for your load, and put 1 or 2k ohms in series with the base, and you should be ready to go. One last caveat- inductive loads like mechanical relays have a nasty habit. The coil current keeps flowing for a brief period after the switch is turned off because the magnetic field in the relay coil takes time to collapse. That causes a negative voltage spike that can damage your buffer transistor. Use a diode as a clamp across the relay coil to dissipate any reverse energy. Most relays are available with built-in diode clamps. Recommended.
For loads of more than a few amps, the power dissipation in a bipolar transistor like a TIP41 will become the limiting factor. You don't want too much heating close to your precision data system if you can help it. In that case, you may use a FET switching element instead of a bipolar transistor. FETs can have milliohm resistance when on, which allows them to carry high currents without much self-heating. We have already expanded this seemingly very simple subject into a bit of an exercise, so FETs will await another day.
Tom Lawson
May 2021
|

|
|
| Hunting Ground Loop Gremlins |
|
Posted by: Tom - 04-27-2021, 06:49 PM - Forum: Start Here
- No Replies
|
 |
Ground loops are like gremlins that can plague your circuitry. Ground loops often behave unpredictably and can appear to come and go. They present one of the more challenging trouble-shooting tasks for precision instrumentation. Most discussions of ground loops focus on hum in audio systems. Usually, the ground loop is formed by redundant grounding through shielding and through the third prong of power plugs, with building wiring forming part of the loop. Because any loop is an antenna, and antennas pick up ambient noise, line frequency is then injected into audio signals. We know that problem as hum. The amplitude and frequency of noise pickup in a loop depends on the loop area and geometry as well as nearby sources of ambient noise. It is no wonder that the AC behavior of ground loops is hard to pinpoint.
Fortunately, the DC behavior is easier to understand and track down. When you eliminate DC ground loop errors you will probably solve any AC problems, as well. So here, we will focus on direct current. In lower resolution instrumentation, you can get away with a lot of sloppiness, and those habits die hard. A 12-bit A/D converter resolves one part in 4096. For a 10 volt range, that means one count is about 2.44 mv. If you have a 2.44 ma ground current flowing in a wire with 1 ohm of resistance, that will amount to one count on your A/D converter. An ohm is a fair amount of wire resistance. It takes almost 25 feet of 26 gauge copper wire to get an ohm of resistance. So, unless you are dealing with larger currents or longer wires, in a 12-bit system, you can generally ignore the interconnection resistance, and think of wires as ideal conductors.
That is not so in high resolution systems. A 24-bit A/D resolves to better than a microvolt on a 10 volt range. That means that milliohms of resistance show up in your voltage data when milliamps of current flow. Whenever any current is flowing, connecting two points with a wire does not mean that the two points are at the same DC potential. That truth is counterintuitive. The fiction of equi-potential connections obscures the source of many grounding problems.
Further, in practical systems, loads are switched on and off. Valves, fans, heaters, motors or pumps cycle as an instrument operates or a process proceeds. Those switched loads involve more than enough current to alter the relative “ground” potentials in a system. Those changes interact with the geometry of interconnection to change where currents flow. If ground loops are present, seemingly mysterious behavior is not unexpected. Here is a simple example simulated in LTSpice.
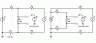
Start with a switched load and some control circuitry shown as a dotted box. On the left, the power supply connections are daisy-chained. On the right, each circuit has its own connections back to the 10 volt power source. The wires are shown as 1 ohm resistors and the switched load is one amp. Yes, that may be a bit strong, but the effect here is volts, so if your currents are milliamps instead of amps, the effect will still be millivolts.

The upper trace shows 2 volts of interaction in the difference between the V1 and V2 terminals of the control circuit, which is illustrated here as a dotted box. That large change is the result of the two one ohm resistors in series with the one amp switched current. The lower trace shows 2 to 3mv of non-ideality. The 1 mv step is seen because the voltage source is not perfect. (Like zero resistance wire, perfect voltage sources are hard to obtain in the field.) This voltage source has a one milliohm of source impedance, causing a 1 mv change with the one amp load step. Then, because the 10K resistor in the dotted box draws essentially one milliamp from the 10 volt source, each of the other two 1 ohm resistors have a one millivolt drop across them. Even so, the difference between the properly wired right-hand circuit is three orders of magnitude better than the left-hand circuit.
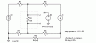
Now, we can insert a ground loop. The ground loop is represented by the new resistor in the center bottom. To make the effect dynamic, the resistance is calculated, as the variable {rx}. The .step function increases the resistance from 1 ohm to 1.2 ohms in 200 milliohm increments with a different color trace for each. That resistance change is to represent the tempco of copper. (More on that below.) Because the new current path of the ground loop partially bypasses the original current return path for the switched load, the interaction with the differential voltage, Dif, is altered as seen in the resulting waveforms. The lower waveform is the same as the one above, but with the vertical scale magnified. Note that the DC interaction only occurs when the load is on.

It might seem that the interaction is reduced, but remember that the ground loop can come and go erratically. Further, when copper wire heats, its resistance goes up. When current is flowing in the wrong path, the wire can heat quite a bit. I know I have melted through insulation of a misplaced ground wire on more than one occasion. Copper has a tempco of 0.4% per deg. C. Since it takes many dozens of degrees to melt the insulation off of wire, you see that the resistance can change quite a lot. As a result, excess current can heat up the ground loop path, increasing its resistance enough to incline the current to find an alternate route. Different size wires will heat at different rates, so currents in different paths can be changing when it might seem that conditions should be static. Then, loads turn off or on, and the situation changes again. Think of multiple loads and loops and multiple warming and cooling wiring paths all interacting in indeterminate fashion. You would see slow thermal oscillations mixed with other DC effects. It would be non-trivial to simulate all that, but it is not hard to imagine.
Further, the switched load that alters the ground currents doesn't even have to be in your system. It could be elsewhere in the building, but plugged into the same AC branch circuit. There may be one earth ground for an entire building, so currents there can interact in more seemingly mysterious ways. Ground loop problems can come and go with the time of day or the season, following the building's HVAC system, or lighting requirements.
When you factor back in the AC effects, it is no surprise that the gremlins can appear to be in control. Your defense is proper wiring practice. It might seem like unnecessary extra bother to pay proper attention to system wiring, but that is the influence of the gremlin on your shoulder whispering bad advice in your ear.
Tom Lawson
April 26, 2021
|

|
|
| The History and Future of Artificial Intelligence - A Reflection |
|
Posted by: Tom - 04-16-2021, 03:20 PM - Forum: Start Here
- No Replies
|
 |
In the late 1970s I worked on simulating predator/prey interactions on Apple][ computers. An underlying requirement was a random number generator. The built-in RND function was not good enough because it would always produce the same sequence given the same starting point. When you subject results to statistical analysis, you are looking for hidden correlations, not for underlying patterns in your supposedly random methods. The initial challenge was simulating the behavior of a housefly on a windowpane. That task falls neatly into what can be easily visualized on a computer monitor and doesn't seem to require too much intelligence. After all, how smart is a housefly?
Statisticians have a wonderful term for such random-seeming behavior - the drunkard's walk. It turned out that seemingly simple rules could produce what looked like very complex behavior. Remember when fractals were trendy? It also turned out that even with a proper random number generator, it took a fair amount of calculation in order to produce what looked like mindless blundering. It also made very clear that any results were the consequence of the underlying assumptions that were implicit in the rules. How much should the last step size or direction or update rate affect the next step? How do the rules interact with the screen edge? Are there longer-term dependencies? For example, does the fly tire? Does the fly stick to the same rules, or does it change its behavior after a period of time? Even the very simple is not necessarily as simple as it seems.
When simulating that "simple" behavior, the computer was slower than a housefly. The random number generator needed to be coded in machine language for the fly to move at all naturally. That gave me a new respect for how primitive computers were in comparison to real life. Back then, we spoke of hardware, software, firmware and wetware. (You don't run into the term wetware very often these days outside of science fiction. The AI promoters prefer different vocabulary.) Of course, modern computers can run circles around an Apple][ computer, but the tasks that modern AI attempts are vastly more complex than simulating a fly on a windowpane.
Another reality of simulation is that it needs to be faster than life in order to be more than an academic exercise. If your AI weather forecasting model is slower than real-time, your forecasts will predict yesterday's weather. There is not a lot of demand for that. Still, conscientious model makers update their models so that they "predict" past events accurately. Yes, that refinement process improves the models, but it also produces the illusion that the models are excellent predictors of unknown future events. That is only the case when things stay generally the same. If anything actually changes, the models will almost infallibly under-predict the effect.
When you hear projections of how Artificial Intelligence is going to help us solve the problems of the future, remember the fly on the windowpane. Even a dull person would use the door if they wanted to go outside. It all comes down to how you frame the problem.
Tom Lawson
April 2021
|

|
|
|