| Welcome, Guest |
You have to register before you can post on our site.
|
| Online Users |
There are currently 10 online users.
» 0 Member(s) | 10 Guest(s)
|
| Latest Threads |
Thoughts on Obsolescence,...
Forum: Start Here
Last Post: HerbertDaf
09-05-2022, 04:55 PM
» Replies: 1
» Views: 10,123
|
A Brief Exploration of Bo...
Forum: Start Here
Last Post: Tom
04-05-2022, 04:10 PM
» Replies: 0
» Views: 2,485
|
The Fundamentals of Digit...
Forum: Start Here
Last Post: Tom
03-17-2022, 04:34 PM
» Replies: 1
» Views: 3,578
|
The Fundamentals of Digit...
Forum: Start Here
Last Post: Tom
03-15-2022, 08:32 PM
» Replies: 0
» Views: 2,491
|
The Fundamentals of Digit...
Forum: Start Here
Last Post: Tom
03-14-2022, 05:39 PM
» Replies: 0
» Views: 3,048
|
The Fundamentals of Digit...
Forum: Start Here
Last Post: Tom
03-10-2022, 07:23 PM
» Replies: 0
» Views: 2,229
|
Fundamentals of Digital E...
Forum: Start Here
Last Post: womantops660
03-10-2022, 07:29 AM
» Replies: 1
» Views: 3,249
|
What Does It Take to Get ...
Forum: Start Here
Last Post: Tom
02-21-2022, 04:36 PM
» Replies: 0
» Views: 2,531
|
Some History of Loop Cont...
Forum: Start Here
Last Post: Tom
12-24-2021, 02:49 PM
» Replies: 0
» Views: 2,305
|
Some History of Loop Cont...
Forum: Start Here
Last Post: Tom
12-17-2021, 04:23 PM
» Replies: 0
» Views: 2,240
|
|
|
 Drawing the Analog to Digital Line in LTSPICE, Part 1
Drawing the Analog to Digital Line in LTSPICE, Part 1 |
|
Posted by: Tom - 02-22-2021, 04:33 PM - Forum: Start Here
- No Replies
|
 |
Having given some thought to the somewhat fuzzy distinction between the analog and digital realms, let's use SPICE to better visualize the transition. First, here in part 1, we will start from the digital side, and move toward increasingly analog.
A simple sine function in a SPICE behavioral provides the point of departure. The idea is to split the waveform into an increasing number of discrete steps. The SPICE variable time provides the steadily increasing value. V = sin(time) in a behavioral produces the familiar sine waveform, +/- 1 volt, centered on zero volts. The number of discrete steps we will divide the waveform into must be an integer.
The expression int(time) accomplishes that task via the truncation offered by the integer function. If the integer number of steps for a one volt sine wavel is 2, a digital representation of the sine function would be zero, plus 0.5, zero, minus .5, zero, etc. As the integer number of steps increases, the sine function smooths out, until eventually, it looks entirely analog. The whole expression would fit into a single SPICE behavioral except that time keeps advancing. We multiply by time, truncate and then divide by time. If time changes during the process, it would create artifact. So, we need two SPICE behaviorals, one for the time, t, and one for the waveform, aatodd, indicating an attenuated A to D conversion.

Fig. 1
The formula for t results in an integer, starting with one, and counting up a tick every ten seconds. The formula for aatodd multiplies the sine times that integer, truncates the result, and then divides by that same integer. The .tran statement below defines the SPICE run - transient analysis from 0 to 1500 seconds, with a maximum timestep of 200us.

Fig. 2
Above is the first 80 seconds of the output. The maximum truncated value goes from nothing, to 1/2, to 2/3, to 3/4, etc, as the number of steps increases. By 80 seconds elapsed, there are 7 steps on the positive side, and seven steps on the negative, and the maximum value is 7/8. That might be called a “3 bit plus sign” A/D converter.

Fig. 3
By 1000 seconds out, value t is 100, so there are 100 steps for each polarity. We are still short of 8 bits of A/D conversion, which would require 2 to the 8th, or 256 steps. Even so, the waveform is now distinctly analog to the eye. The peak values now are 99/100ths, or 0.99 volts. We have made it to 1%.

Fig. 4
A drastic expansion of the waveform shows that the individual steps are still discrete and digital. The cursors show that one step is now 9.9 mv. The actual number is 10 mv. 1 volt/ 100, but the pixelation of the screen limits the resolution. That is just another form of the same phenomena.
In SPICE, we can run the resolution up to an extreme, arbitrary level, although analysis slows down when you calculate out all those decimal places. In practical circuits, noise becomes an increasing intrusion. Every time you add a bit the the digitization, you need the noise floor to be twice as quiet.
We have here used SPICE as a visualization and teaching tool, not for circuit design. Does anyone have other examples to share of using SPICE for teaching abstract concepts?
Next time, we will start from a pure sine wave and morph it into a square wave.
Tom Lawson
February 22, 2021
|

|
|
| Why is it Called Ground or Earth, and What is Common Mode Rejection? |
|
Posted by: Tom - 10-06-2020, 03:22 PM - Forum: Start Here
- No Replies
|
 |
Early telegraph systems used one wire, strung on poles. The circuit was completed at each end of the single wire by making a
connection to the earth, which is conductive. That connection was variously called earth, ground, common, or return. It was not
always easy to get a good ground connection. If a rod driven into the earth was not sufficient, a plate could be buried, to get more
surface area. Even with a good connection to the ground, the potential of the earth is not everywhere the same, so rather large
telegraphic signals were required for reliable communications.
These single wire systems worked well-enough until the introduction of the electric tram. The disturbances caused by trams in the
earth's potential swamped the largest telegraphic signals. The solution was to run a second wire, originally called a metalic return.
The return was also referred to as a ground wire, or simply, earth. Then, the telegraphic signals were detected across two wires,
instead of between one wire and the literal earth. One company that rose as a result of this improvement became A, T & T.
The difference between the single wire system and the two wire telegraph system reflects the distinction between "single-ended" and
"differential" and it matters because "ground" is not simply zero volts. In fact, any two points designated "ground" will have AC and
DC voltages present between them that can easily become non-trivial. In a switched power system with fast edges, we have seen 50
volt spikes developed across a 1/4 inch diameter, 1/2 inch long aluminium standoff. Those spikes were an AC effect due to
self-inductance, not resistance, but if you want to measure DC down to the uVolt, you need to pay attention to uOhms. If you want
high precision analog measurements, get used to the notion that "ground" is relative, not absolute.
We modify our wiring schemes to minimize these grounding effects. Star grounding brings many wires to a "single point" ground.
That approach certainly helps to minimize ground potential differences, but having a separate conductor from each ground to a
single point in a large system is physicaly impossible. Plus, ground wires have resistance and self-inductance in proportion to their
length. So, we make do, and "ground" ends up being a range of voltages centering around zero.
To measure a voltage with real accuracy, the measured voltage has to be a difference between the potential at two points.
Otherwise, the variation in "ground" potential adds to any other errors. That differential nature is more intuitive when you use a
battery-powered digital voltameter. The reading on the meter is the voltage difference between the potential at the black lead and
the red lead. Earth potential does not enter into it.
A precision analog-to-digital converter will have a true differential input, which amounts to the very much the same thing. There is
one additional factor for high input inpedance circuits. The meter may only have a few megohm input impedance, if you need to
not load down the voltage being measured, you need thousands, or millions of megohms input impedance. That requires a buffering
circuit, and the buffer in turn, requires a power supply. The buffer circuit will only operate properly when the input is between its
power supply voltages. Sometimes the buffer's input range is more limited than that. This specification is called the common mode
input range, and it is a voltage range referenced to the ground voltage as seen by the buffer circuit, which may, or may not, be
close to "earth" ground.
The other key specification is Common Mode Rejection Ratio (CMRR) which quantifies the insensitivity to voltages that appear on
both the input wires of a differential input. It is expressed as a ratio, in decibels (dB). It is logarithmic in nature. The formula is 20
times the log of the ratio. If a circuit passes 1/10 of any common mode voltage, it has a common mode rejection ratio of -20dB. If
a circuit passes 1/100 of any common mode voltage, it has a common mode rejection ratio of -40dB, etc.
To get best accuracy, you need to use differential inputs, you need to take care to minimize the common mode noise, and you need
an A/D converter with good common mode rejection. But first and foremost, you need to remember than "ground" is at a
different potential every place you drive your stake into the earth.
Tom Lawson
October 2020
|

|
|
| Simulating a Simple Delta Sigma modulator |
|
Posted by: Tom - 10-02-2020, 04:07 PM - Forum: Start Here
- No Replies
|
 |
The Model 203 and Model 333 are Delta Sigma converters built from discrete parts. First, why would we bother to do that? Back
during a boom period in the 90's I tried to order Delta Sigma converter chips from one of the major manufacturers. They said the
lead time was one year. I said yikes! Please place my order. They said, sorry, our system only goes out to 364 days, we can't
accept an order.
So, we designed and built the Model 203, a Delta Sigma converter that uses only ordinary, available parts. It has an RS-232
interface. A few years later, we added the Model 333, which is similar, but with a USB interface. The heart of a Delta Sigma A/D
converter is a modulator. A simplified SPICE version of the modulator is shown as Fig 1. The clock is in the lower left. It runs at 10
MHz. The analog input is at the upper left. In the center is a D-type flip/flop paced by the clock. The data to the flip/flop is the output
of a comparator that looks at whether the summing junction is above or below zero volts.
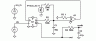
The summing junction is the combination of two signals, filtered together by series resistors and capacitor C1. The upper signal is
the analog input voltage, offset by -5 volts. The lower signal is the output of the flip/flop. The purpose here is to match the average
output of the flip/flop to the input voltage. In SPICE, logic signals can be ideal. In reality, the flip/flop output must be buffered to
produce a near-ideal logic 1 (5 volts) or logic 0 (0 volts). If the summing junction is positive, the data is a one. If it is negative, the
data is a zero. The result is a continuous string of ones and zeros at the point labeled Out. These are counted and filtered digitally
to obtain the conversion results.
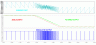
In Fig 2 that data Out is seen on the lower axis, labelled Modulator Output. The analog input, in red in the middle, starts at just
below the maximum value, then slews rapidly to just above the minimum value. Notice that the output data is almost always high at
first, and almost always low after the transition. The summing point is shown as the top trace. You can see that the 25us transition
period gives the system a little trouble. It can't quite keep up, so the summing junction jumps around showing a little sub-harmonic
behavior. That is not really a problem in a DC sense, because any errors get fed back and cancelled out.
The green trace is a filtered version of the output signal. It is not needed, and is not actually part of a Model 203 or 333, but it
does illustrate the validity of the modulator. Notice that during the rapid slew, the green trace does not perfectly follow the input
trace, even after allowing for the slight filter delay. That non-ideality shows the limits of the AC, or dynamic, reponse of this
particular Delta Sigma modulator. In practice, this circuit gives 20-bit performance for low frequency signals, and its frequency
response is set up to cut off sharply at 60 Hz. In Europe, a software constant is changed to move the cutoff to 50 Hz.
The simulation is a big help for understanding and design, but simulating the parasitics and other stray effects is as much an art as
a science. At some point, you need to move to the bench.
Tom Lawson
October 2020
|

|
|
| Thoughts on the Digital Revolution |
|
Posted by: Tom - 10-01-2020, 04:58 PM - Forum: Start Here
- No Replies
|
 |
In the 1970s digital electronics began taking over from analog electronics. The most conspicuous form was the
personal computer, but it went far beyond that. At the time, I was working for a medical electronics company. One of
our products was a Cardiac Output Computer. It calculated cardiac output from a dye dilution curve using analog
multiplier divider circuitry. The logic was mostly implemented in a large multi-wafer rotary switch with dozens of
interwired contacts. The result would appear on a large, old-school meter face which took up most of the front of the
instrument.
A bolus of dye was injected near the heart of a catheterized patient and sampled at a downstream artery with a pump
and a detector called a densitometer. The dye would appear as a peak with an exponential decay. Some of the dye
would take a shorter route back to the heart and would appear a second time, called recirculation. Recirculation would
cause the decreasing dye curve to reverse direction. Cardiac output was calculated from the area under the curve,
absent recirculation. The challenge was that integration of that area under the curve got more and more complete a
time went on, but from the moment recirculation hit, the area under the curve no longer represented the cardiac
output. In order to estimate what the area would have been without recirculation, the integral representing the past
area was summed with a differential term repesenting the predicted area under the curve if the exponential decay
continued.
The answer improves with time because the total area calculation consists more of the integral history and less of the
differential prediction. Then, when recirculation starts, the curve bends upward, and the differential term gets huge.
At that point the prediction becomes meaningless.
The doctor injected the dye and watched the meter settle to the answer, then the needle hit the peg upon
recirculation. The doctor's confidence in the answer went up to the extent that the needle was steadier for longer.
Simple enough, and quite intuitive.
One day the head of sales came into the engineering department with a nixie tube in his hand and said digital is the
new big thing. Sure, we responded, we could replace the big meter with a three-digit digital display. We did that, but it
wasn't quite the whole story. A a changing digit tended to look like an 8, regardless, because all the segments lit up
fast and dimmed down slowly. Ok, that meant we needed to latch the answer, which didn't seem like it should be too
hard. We were wrong. If you latched too soon, you would get a substandard reading and if you latched too late you
would have no reading. Plus, the doctor no longer knew how much confidence to place in the answer.
The conclusion was that we needed to calculate a set of possible answers and evaluate them statistically to obtain a
confidence level. Enter a microprocessor. In those early days we needed to design our own development system. We
needed to create our own tools, down to needing to write our own floating point math routines in assembly language
(there was no higher level language for microcomputers yet) for the statistics.
Complexity went through the roof. Do you iterate and rank different possible answers then pick the best? Do you
report both an answer and a confidence level? How long will the doctor wait for your primitive computer to grind
before he/she complains to the salesman that it is too slow and he liked the analog computer better?
In the end, the switch to digital computation surely improved the results, but there was a long, uncomfortale period
between pure analog and mostly digital when a successfull transition was no sure thing. It is easy to forget that, in
retrospect.
Tom Lawson
October 2020
|

|
|
| Different Control Loops Have More in Common than You Might Think |
|
Posted by: Tom - 09-30-2020, 02:28 PM - Forum: Start Here
- No Replies
|
 |
Having worked around operational amplifiers since the advent of the uA709 integrated amplifier and around all manner of controls for various sorts of instrumentation, I thought that controls to regulate a switched-mode power converter would be an entirely different matter. Only after internalizing the problems encountered, and after 10 years of learning, did I realize that the underlying problem was the same. Whether you are controlling temperature with a loop running at 1 Hertz, or regulating a power supply voltage with a loop running at 100 kHz, the problem with trading off between stability and speed of response is fundamentally linked. The problem reduces to delayed feedback.
The terminology is different for different fields, but whether you are compensating an op amp or tuning a PID loop, you are changing the response of a feedback loop to get around the problem of delayed response causing a tendency toward oscillation. The answers we found for power converters involved prediction, which moved the filter delay to outside of the feedback loop. It was a pleasant surprise to discover that the same concept, applied to PID type loops, was a huge help.
Operational amplifiers have specs for bandwidth. open loop gain, slew rate, small signal response, large signal response, unity gain stability, and capacitive load tolerance, and on and on. These are some of the factors relating to that loop compensation, which is the tradeoff between stability and agility. Switched-mode power converter control loops have to remain stable in the face of an analogous set of varying conditions, made worse by the discontinuous feedback in many power supply topologies. A deterministic prediction enables uncompromised dynamic response by removing the loop delay. We call that breakthrough Predictive Energy Balancing, or PEB.
For power converters, the PEB technology is patented, but that same learning underpins the free data acquisition and control templates that we provide. We make it easy to take advantage of a lifetime's work.
Tom Lawson
|

|
|
| Thoughts on Obsolescence, Planned or Otherwise |
|
Posted by: Tom - 09-29-2020, 01:56 PM - Forum: Start Here
- Replies (1)
|
 |
Technology has changed dramatically over the last 50 years. Inevitably, that change will bring with it obsolescence. There is a difference between things that are intentionally obsolete for convenience or profit compared to things that have earned obsolescence by outliving their usefulness. Age alone does not equate to lost utility. A 50 year old car may be prized as an antique, and it may be more fun to drive than a modern car. A high fidelity tube audio amplifier from 1970 may be particularly prized today by audiophiles.
In the arid, remote West, the dumps of abandoned homesteads tell forgotten stories of fashion and obsolescence. It is not uncommon to find a wood-fired cook stove in the kitchen and a "modern" propane-fired stove in the dump. The chronology can be reconstructed from the evidence. The original wood-fired stove was replaced with a fashionable propane stove. Over time, the propane stove was found to be less satisfactory than the wood stove. Maybe the cost of propane went up, or the propane burners needed frequent maintenance. At some point, the homesteader salvaged the wood stove from the dump and deposited the propane stove in its place. As an engineer might observe, progress is not always linear.
In the computer business, the flip side of planned obsolescence is backward compatibility. Backward compatibility is not quite as cut and dried as a one or a zero. The Apple ][ GS was billed as 100% backward compatible to the Apple ][, but its commercial failure cast a shadow over the future of open systems with strict backward compatibility. The Apple ][ yielded to the Mac, which was a closed, incompatible system. That heralded an unfortunate trend for an age when we are running out of resources and are choking on our own discards. If you wanted to add function to your Apple ][, often you could plug an expansion card into an expansion slot. If your Mac wasn't up to the job, it was time for a new computer. Lack of expandability is a step short of intentional obsolecence, but there are plenty of examples of completely satisfactory computers becoming landfill due to new software requirements that amount to little more than thinly disguised intentional obsolescence. I am not singling out Apple, here. A perfectly good Windows computer gets upgraded to the latest operating system, but over time problems develop and the computer becomes baulky and unreliable. The old operating system is, by then, no longer supported, so it's time for a new computer. We have been conditioned to expect shockingly short useful lives out of expensive computers. At this point the situation has gotten out of hand. Electronic waste is an industry-wide problem, and planned obsolescence imposes an industry-wide cost to society as well as an aggravation for its victims.
So what can be done, practically speaking? To start with, products can be designed for long life. That entails using established, high quality components and uncompromised construction. Long-lived products are designed for survivability and serviceability. If a system needs repair, the older it is, the more likely it will be discarded, even if it could be economically repaired. So, for example, don't just recommend a surge-protected plug strip, build in surge protection. Remember that it helps to design in expandability, and to document the product while minimizing the need for unstated context, so that interested parties in the future can make sense of the documentation. The fewer assumptions about specific uses or backgrounds, the better. A long-lived product will do basic things well and conveniently, not just fill a narrow need, or aim at a particular market window.
Software can be can kept backward compatible with just a little extra care, unless there are major operating system changes. Historically at Lawson Labs, we have provided dlls with documentation to simplify communications with the hardware. In many cases, replacing an older dll with a newer one is the only change needed when migrating to a newer operating system. That eliminates one class of obsolescence. It is not unusual to have special, in-house software that was written by someone who has left the company, or that requires a particular compiler that is no longer functioning. If changes are required to get that software to run on a newer computer or operating system, it can trigger the death knell of the custom software, which, in turn, obsoletes the hardware. If instead, substituting a free dll update solves the compatibility problem, we have achieved a major convenience with commensurate cost savings. Plus, the landfill gets a break.
Also, please be in touch if you have a 1970 E-type you don't want around any more.
Tom Lawson
|

|
|
| Oversample and average to get good resolution, or not |
|
Posted by: Tom - 09-28-2020, 01:18 PM - Forum: Start Here
- No Replies
|
 |
Why do I need an accurate A/D with good specs when I can just average the data from a hobby A/D and get to the same resolution?
Yes, you can get the appearance of high-resolution data from heavily averaged noisy, or lower quality data, but it doesn't carry much meaning. Why?
First, a self-evident point. The linearity will be limited by the linearity of the underlying data. Attempting to make a straight line out of a crooked one is a little like straightening a nail with a hammer. Be careful of your fingers, and don't be surprised if you lose the nail, entirely.
Second, any asymmetry will skew your results. Take a simple example, a one-bit A/D. Let's say you feed a symmetrical sign wave, from 0 to 5 volts, to a one-bit A/D, i.e. a comparator, that nominally switches at 2.5 volts. You then accumulate a long series of one-bit conversions. Ideally, half the results will be ones and half zeros. If you took a million points, the averaged conversion result would ideally be 500 thousand ones out of one million bits. If there is any offset in the comparator, that will offset the results. Then, if the comparator responds faster to positive or negative transitions, that will skew the results further. Also, if the input drifted a tad into one or the other stop, that would distort the waveform and skew the results. If there is a buffer for the input signal that slews at a different rate up and down, that will skew your results, etc.
Third, any stray feedback will interfere. That stray feedback could appear in the signal, causing, say, an output of one to capacitively couple back to increase the input magnitude. Remember, the stray effect only needs to be a few parts per million to show up in your results. Or, that stray feedback could act through the power supply, perhaps causing the switching reference voltage to drop slightly when the output was already a one. That stray feedback could be thermal. More switching at the comparator would cause self-heating, which could change the comparison point. Positive stray feedback will cause oscillation. Negative stray feedback will amplify. Neither will improve the stability or accuracy of your system. In practice, all these things happen, and more. I know from building Delta Sigma converters that use a one-bit D/A and a clocked comparator followed by a digital filter to extract a high resolution result. In order to get 20-bit data out of such a converter, you need 20-bit precision in the D/A. There is no free lunch.
So, if you think you can make a 20-bit A/D out of a 16-bit A/D by oversampling and averaging, think again.
Tom Lawson
|

|
|
| Getting Started |
|
Posted by: Tom - 09-24-2020, 07:12 PM - Forum: Start Here
- No Replies
|
 |
We are kicking off a discussion board for data acquisition and control subjects. We will start from Lawson Labs products, but will not limit ourselves to them. Data Acquisition and Control in the past was the focus of trade publications, national trade shows, and a variety of local conferences and table-top shows. Recently, the subject is mostly treated piecemeal, on an industry-by-industry basis.
Our purpose here is to create a resource for anyone interested, from hobbyist to expert, in data sytems designed to to be understood, instead of just operated by a user. We will begin with a focus on control, largely because we offer free acquisition and control spreadsheet templates that deserve a wider audience. Here is an introduction:
http://www.lawsonlabs.com/whitepapers/Ge...ontrol.pdf
Questions and comments are welcomed.
UPDATE: We have found the bulletin board format to be constantly assailed by spammers and would-be con men. Instead of logging in, please address your comments to lawsnlab@lawsonlabs.com, and we will move appropriate discussions to this platform.
Thank you,
Tom Lawson
|

|
|
|